Có bao nhiêu giá trị thực của tham số \[m\] để đồ thị hàm số \[y = \frac{{{x^2} - 1}}{{{x^2} + \left( {2 - m} \right)x + 2m + 1}}\] có đúng hai đường tiệm cận?
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 1 (có lời giải) !!
Quảng cáo
Trả lời:
Đáp số: 3.
Ta có: \[\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{x^2} - 1}}{{{x^2} + \left( {2 - m} \right)x + 2m + 1}} = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{1 - \frac{1}{{{x^2}}}}}{{1 + \left( {2 - m} \right)\frac{1}{x} + \left( {2m + 1} \right)\frac{1}{{{x^2}}}}} = 1\]
Suy ra đồ thị của hàm số đã cho có đường tiệm cận ngang \[y = 1\], do vậy đồ thị đó có đúng 2 đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng một đường tiệm cận đứng
\( \Leftrightarrow \) phương trình \[{x^2} + \left( {2 - m} \right)x + 2m + 1 = 0\left( * \right)\] có nghiệm kép hoặc có một nghiệm \[x = - 1\] và một nghiệm khác \(1\) hoặc có một nghiệm \[x = 1\] và một nghiệm khác \( - 1\).
Trường hợp 1: Phương trình \[\left( * \right)\] có nghiệm kép
\[ \Leftrightarrow \Delta = 0 \Leftrightarrow {\left( {2 - m} \right)^2} - 4\left( {2m + 1} \right) = 0 \Leftrightarrow {m^2} - 12m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 12\end{array} \right.\].
Trường hợp 2: Phương trình \[\left( * \right)\] một có nghiệm \[x = 1\] và một nghiệm khác \( - 1\) \( \Leftrightarrow \left\{ \begin{array}{l}m = - 4\\m \ne 0\end{array} \right. \Leftrightarrow m = - 4\).
Trường hợp 3: Phương trình \[\left( * \right)\] một có nghiệm \[x = - 1\] và một nghiệm khác \(1\) \( \Leftrightarrow \left\{ \begin{array}{l}m = 0\\m \ne - 4\end{array} \right. \Leftrightarrow m = 0\).
Vậy có 3 giá trị của \[m\] thỏa mãn yêu cầu bài toán là \(m = - 4,\,m = 0,\,m = 12\).
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Ta có \[a = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{ - {x^2} - 3x + 4}}{{x + 2}}:x} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} - 3x + 4}}{{{x^2} + 2x}} = - 1,\,\]
\[\,b = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{ - {x^2} - 3x + 4}}{{x + 2}} - \left( { - 1} \right)x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 4}}{{x + 2}} = - 1\]
(Tương tự, \[\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 3x + 4}}{{x + 2}}:x} \right) = - 1,\,\]\[\mathop {\lim }\limits_{x \to - \infty } \left[ {\frac{{ - {x^2} - 3x + 4}}{{x + 2}} - \left( { - 1} \right)x} \right] = - 1\])
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x + 2}}\) là đường thẳng có phương trình \(y = - x - 1.\)
Câu 2
Lời giải
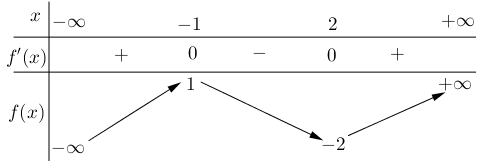
Dựa vào bảng biến thiên, ta có giá trị cực tiểu của hàm số đã cho bằng \( - 2.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số trên đoạn \(\left[ {0\,;\,3} \right]\) bằng A. \(4\). B. \(2\). C. \(3\). D. \(0\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759222372.png)