Cho các hàm số sau \(f(x) = {x^3} - 8{x^2} + 16x - 9\), \(h\left( x \right) = \frac{{{x^2} - x + 1}}{{x - 1}}\).
Trong các mệnh đề sau, đâu là mệnh đề đúng đâu là mệnh đề sai?
a) Giá trị lớn nhất của hàm số \[f\left( x \right)\] trên đoạn \([ - 1;1]\) là \(0\).
b) Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)\) trên đoạn \[\left[ {1;3} \right]\] lần lượt là a, b. Khi đó giá trị của \(27a - b\) bằng \(13\).
c) Giá trị nhỏ nhất của hàm số \(h\left( x \right)\) trên khoảng \((1; + \infty )\) là \(3\)
d) Độ giảm huyết áp của một bệnh nhân sau khi sử dụng thuốc được đo bởi công thức \(G(x) = 0,025{x^2}(30 - x)\) trong đó \(x({\rm{mg}})\) và \(x > 0\) là liều lượng thuốc tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng \(20mg\)
Cho các hàm số sau \(f(x) = {x^3} - 8{x^2} + 16x - 9\), \(h\left( x \right) = \frac{{{x^2} - x + 1}}{{x - 1}}\).
Trong các mệnh đề sau, đâu là mệnh đề đúng đâu là mệnh đề sai?
a) Giá trị lớn nhất của hàm số \[f\left( x \right)\] trên đoạn \([ - 1;1]\) là \(0\).
b) Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)\) trên đoạn \[\left[ {1;3} \right]\] lần lượt là a, b. Khi đó giá trị của \(27a - b\) bằng \(13\).
c) Giá trị nhỏ nhất của hàm số \(h\left( x \right)\) trên khoảng \((1; + \infty )\) là \(3\)
d) Độ giảm huyết áp của một bệnh nhân sau khi sử dụng thuốc được đo bởi công thức \(G(x) = 0,025{x^2}(30 - x)\) trong đó \(x({\rm{mg}})\) và \(x > 0\) là liều lượng thuốc tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng \(20mg\)
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 1 lớp 12 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
\[\left\{ \begin{array}{l}f( - 1) = - 34\\f(1) = 0\end{array} \right. \Rightarrow \mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 1;1} \right]} = 0\], mệnh đề a) đúng.
b) Ta có \(f'(x) = 3{x^2} - 16x + 16;f'(x) = 0 \Leftrightarrow 3{x^2} - 16x + 16 = 0 \Leftrightarrow \quad \left[ \begin{array}{l}x = 4 \notin [1;3]\\x = \frac{4}{3} \in [1;3]\end{array} \right.\)
Khi đó \[\left\{ {\begin{array}{*{20}{l}}{f(1) = 0}\\{f(\frac{4}{3}) = \frac{{13}}{{27}}}\\{f(3) = - 6}\end{array}} \right. \to \left\{ \begin{array}{l}\mathop {\max f\left( x \right)}\limits_{x \in \left[ {1;3} \right]} = \frac{{13}}{{27}} = a\\\mathop {\min f\left( x \right)}\limits_{x \in \left[ {1;3} \right]} = - 6 = b\end{array} \right. \to 27a - b = 19\]. Mệnh đề b) sai.
c) Ta có \(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}};y' = 0 \Rightarrow {x^2} - 2x = 0
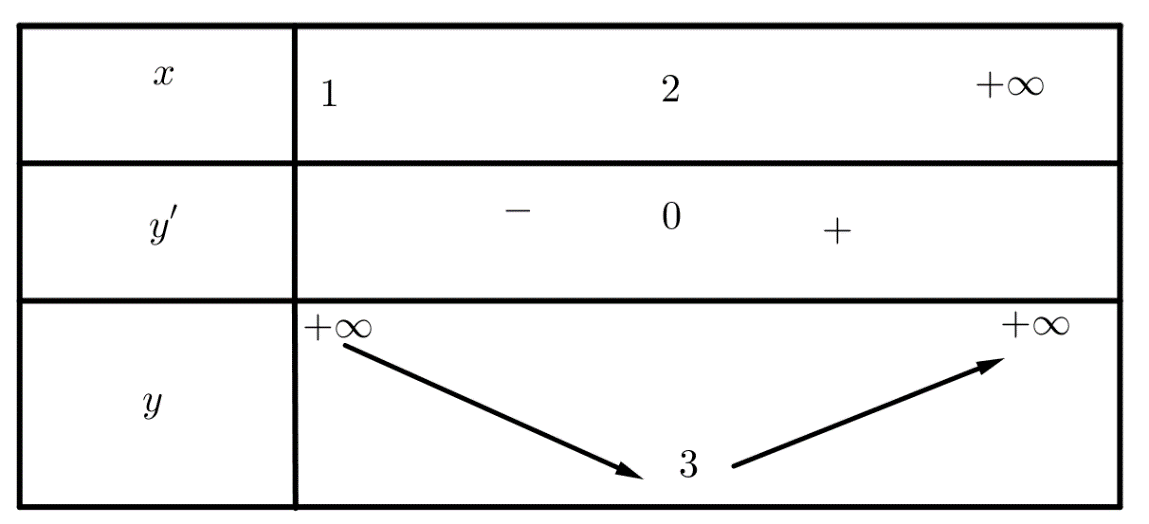
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \notin (1; + \infty )}\\{x = 2 \in (1; + \infty )}\end{array}} \right.\).
Từ bảng biến thiên, suy ra giá trị nhỏ nhất là: 3 \( \to \) Mệnh đề c) đúng.
d) Ta có \[G'\left( x \right) = 1,5x - 0,075{x^2},G'\left( x \right) = 0 \Leftrightarrow 1,5x - 0,075{x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 20 \in \left( {0; + \infty } \right)\\x = 0 \notin \left( {0; + \infty } \right)\end{array} \right.\]
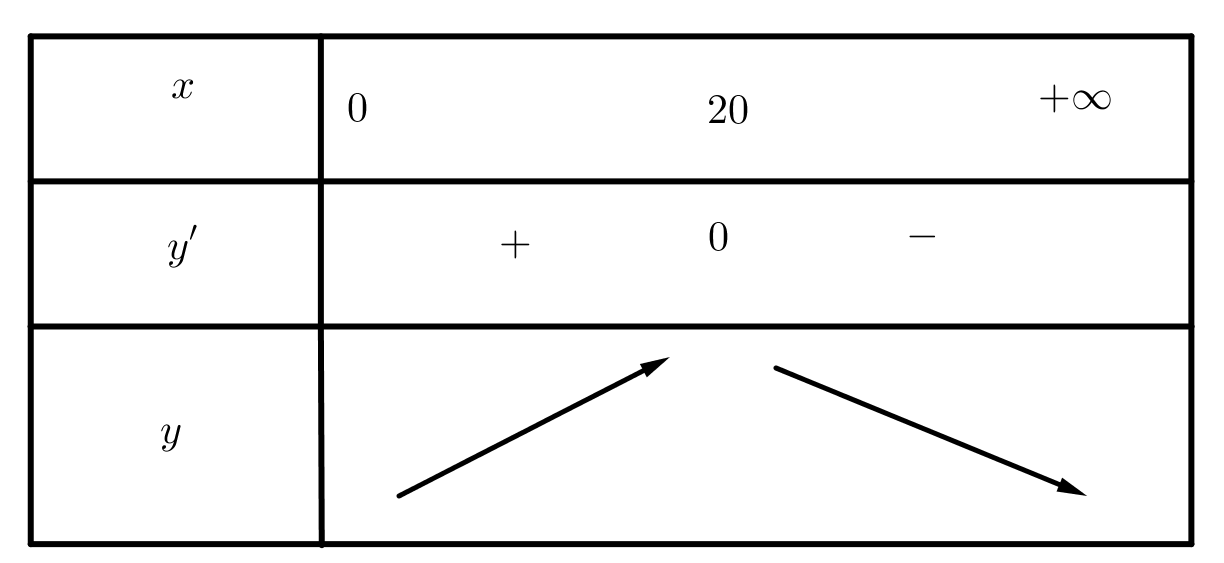
Vậy huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng \(20mg\). Mệnh đề d) đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: \[v'(t) = 0,003906{t^2} - 0,18058t\]
\[v'(t) = 0 \Leftrightarrow 0,003906{t^2} - 0,18058t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 46,23\end{array} \right.\].
\[\begin{array}{l}v(0) = 83;\\v\left( {46,23} \right) = 18,67;\\v\left( {126} \right) = 1254,05.\end{array}\]
Tàu con thoi đạt vận tốc lớn nhất bằng \[1254,05\,\,\,\left( {ft/s} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
\(y = {x^3} - 3{x^2} - 9x + 5\). Tập xác định \(D = \mathbb{R}\).
\(y' = 3{x^2} - 6x - 9\).
\(y' = 0 \Leftrightarrow 3{x^2} - 6x - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.\).
Với \[x = - 1 \Rightarrow y = 10 \Rightarrow A\left( { - 1;10} \right)\].
Với \[x = 3 \Rightarrow y = - 22 \Rightarrow B\left( {3; - 22} \right)\].
Ta có phương trình đường thẳng \[AB\] là: \[\frac{{x + 1}}{{3 + 1}} = \frac{{y - 10}}{{ - 22 - 10}}\] \[ \Rightarrow y = - 8x + 2\] \[ \Rightarrow {x_I} = \frac{1}{4}\]
Vậy suy ra \[\frac{{IA}}{{IB}} = \frac{{\sqrt {{{\left( { - 1 - \frac{1}{4}} \right)}^2} + {{10}^2}} }}{{\sqrt {{{\left( {3 - \frac{1}{4}} \right)}^2} + {{22}^2}} }} = \frac{5}{{11}}\]\( \Rightarrow b + c = 16\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f\left( x \right)\] có đạo hàm trên \[\mathbb{R}\], thỏa mãn \[f\left( { - 1} \right) = f\left( 3 \right) = 0\] và đồ thị của hàm số \[y = (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/11-1759228136.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập