Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\). Hãy dựng các điểm \(M,N\) sao cho \(\overrightarrow {AM} = \overrightarrow {BC} \), \(\overrightarrow {AN} = \overrightarrow {CB} \). Khi đó:
a) \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {BC} \)
b) \(ABCM\) là hình bình hành
c) \(ACBN\) là hình bình hành
d) \(\overrightarrow {AM} ,\overrightarrow {AN} \) là hai vectơ đối nhau
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\). Hãy dựng các điểm \(M,N\) sao cho \(\overrightarrow {AM} = \overrightarrow {BC} \), \(\overrightarrow {AN} = \overrightarrow {CB} \). Khi đó:
a) \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {BC} \)
b) \(ABCM\) là hình bình hành
c) \(ACBN\) là hình bình hành
d) \(\overrightarrow {AM} ,\overrightarrow {AN} \) là hai vectơ đối nhau
Câu hỏi trong đề: Đề kiểm tra Các khái niệm mở đầu (có lời giải) !!
Quảng cáo
Trả lời:
|
a) Sai |
b) Đúng |
c) Đúng |
d) Đúng |
Ta có \(\overrightarrow {AM} = \overrightarrow {BC} \) nên \(\overrightarrow {AM} \) cùng hướng với \(\overrightarrow {BC} \) và \(|\overrightarrow {AM} | = |\overrightarrow {BC} |\), vì vậy \(ABCM\) là hình bình hành (xem hình vẽ). Tương tự, \(\overrightarrow {AN} = \overrightarrow {CB} \) nên \(\overrightarrow {AN} \) cùng hướng với \(\overrightarrow {CB} \) và \(|\overrightarrow {AN} | = |\overrightarrow {CB} |\), vì vậy \(ACBN\) là hình bình hành (xem hình vẽ).
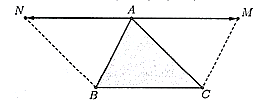
Từ hình vẽ, ta nhận thấy \(\overrightarrow {AM} ,\overrightarrow {AN} \) là hai vectơ đối nhau (\(A\) là trung điểm của đoạn thẳng \(MN\)).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
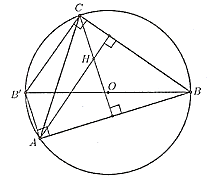
Ta có \(:B{B^\prime }\) là đường kính đường tròn ngoại tiếp tam giác \(ABC\) nên
Mặt khác \(AH \bot BC\), suy ra \({B^\prime }C//AH\) (1).
Tương tự: hay \(A{B^\prime } \bot AB\) mà \(CH \bot AB\) nên \(CH//A{B^\prime }(2)\).
Từ (1) và (2) suy ra tứ giác \(A{B^\prime }CH\) là hình bình hành.
Vì vậy: \(\overrightarrow {AH} = \overrightarrow {{B^\prime }C} ;\overrightarrow {A{B^\prime }} = \overrightarrow {HC} \).
Lời giải
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
Gọi \(M,N\) lần lượt là trung điểm cạnh \(BC,AB\).
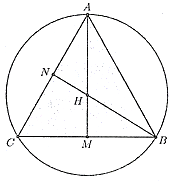
Do tam giác \(ABC\) đều nên \(AM,BN\) cũng là các đường cao của tam giác \(ABC\); vì vậy \(H\) vừa là trực tâm vừa là trọng tâm tam giác này.
Áp dụng định lí Py-tha-go cho \(\Delta ABM\), ta có: \(A{M^2} = A{B^2} - B{M^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\)
\( \Rightarrow AM = \frac{{a\sqrt 3 }}{2}{\rm{. }}\)
Theo tính chất trọng tâm, ta có: \(AH = \frac{2}{3}AM = \frac{2}{3} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\).
Dễ thấy ba vectơ \(\overrightarrow {HA} ,\overrightarrow {HB} ,\overrightarrow {HC} \) có độ dài bằng nhau:
\[|\overrightarrow {HA} | = |\overrightarrow {HB} | = |\overrightarrow {HC} | = AH = \frac{{a\sqrt 3 }}{3}{\rm{. }}\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.