Cho \(M = 5\) và \(N = \frac{{\sqrt {50} }}{2}\). Khẳng định nào sau đây là đúng?
Câu hỏi trong đề: Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 3 có đáp án !!
Quảng cáo
Trả lời:
Chọn D
Ta có \(N = \frac{{\sqrt {50} }}{2} = \frac{{5\sqrt 2 }}{2} = \frac{5}{{\sqrt 2 }} < 5 = M\).
Vậy \(M > N\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thay \(x = 180\) vào công thức \(h = 0,4\sqrt[3]{x}\), ta được:
\(h = 0,4 \cdot \sqrt[3]{{180}} \approx 2,26\;\,({\rm{m)}}{\rm{.}}\)
Vậy chiều cao của hươu cao cổ là \(2,26\;\,{\rm{m}}\).
Đáp án: 2,26.
Câu 2
Lời giải
Chọn C
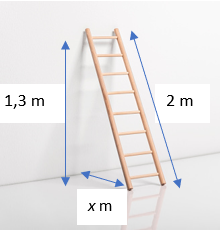
Áp dụng định lý Pythagore, ta có: \[{x^2} + {1,3^2} = {2^2}\].
Suy ra \[{x^2} = {2^2} - {1,3^2} = 2,31\].
Do đó, \[x = \sqrt {2,31} \approx 1,5\,\,({\rm{m)}}{\rm{.}}\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.