Tam giác \[ABC\] có \(BC = \sqrt 5 \), \[AC = 3\] và \(\cot C = 2\). Tính cạnh \[AB\]
Tam giác \[ABC\] có \(BC = \sqrt 5 \), \[AC = 3\] và \(\cot C = 2\). Tính cạnh \[AB\]
A. \[6\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 10 có đáp án !!
Quảng cáo
Trả lời:
Chọn C
Từ giả thiết \(\cot C = 2\), ta suy ra \(C\) là góc nhọn\[\cot C = 2 \Rightarrow \tan C = \frac{1}{2} \Rightarrow {\cos ^2}C = \frac{1}{{1 + {{\tan }^2}C}} = \frac{1}{{1 + {{\left( { - \frac{1}{2}} \right)}^2}}} = \frac{4}{5} \Rightarrow \cos C = \frac{2}{{\sqrt 5 }}\]\(AB = \sqrt {A{C^2} + B{C^2} - 2AB.BC.\cos C} = \sqrt {{3^2} + {{\sqrt 5 }^2} - 2.3.\sqrt 5 .\frac{2}{{\sqrt 5 }}} = \sqrt 2 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
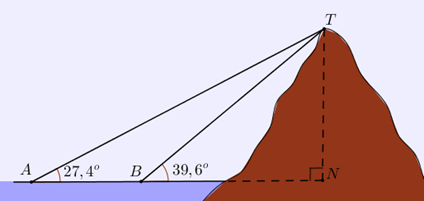
Ta có \(\widehat {ATB} = \widehat {TBN} - \widehat {TAN} = 12,2^\circ \).
Áp dụng định lí sin cho tam giác \(TAB\): \(\frac{{TB}}{{\sin \widehat {TAB}}} = \frac{{AB}}{{\sin \widehat {ATB}}} \Rightarrow TB = \frac{{AB.\sin \widehat {TAB}}}{{\sin \widehat {ATB}}}\).
Xét tam giác vuông \(TBN\) ta có:
\(TN = TB.\sin \widehat {TBN} = \frac{{AB.\sin \widehat {TAB}.\sin \widehat {TBN}}}{{\sin \widehat {ATB}}} = \frac{{1536.\sin 27,4^\circ .\sin 39,6^\circ }}{{\sin 12,2^\circ }} \approx 2132,14\).
Vậy chiều cao ngọn núi xấp xỉ \(2132,14\) m.
Câu 2
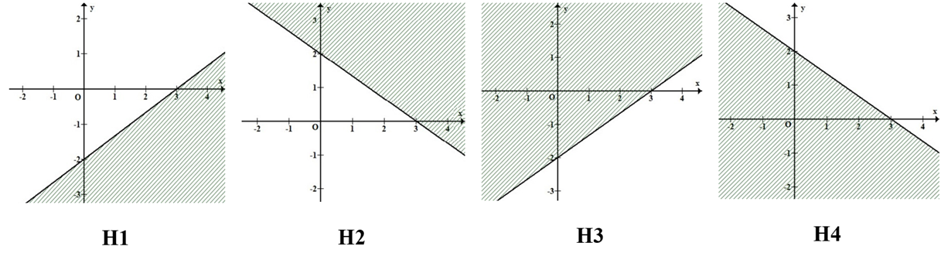
A. H2
Lời giải
Chọn C
Đường thẳng \(2x - 3y - 6 = 0\) đi qua hai điểm \(\left( {0; - 2} \right),\left( {3;0} \right)\) nên loại đáp án H2 và H4.
Mặt khác \(O\left( {0;0} \right)\) không thỏa mãn \(2x - 3y - 6 \le 0\) nên chọn hình H3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[17,3{\rm{m}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {2;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
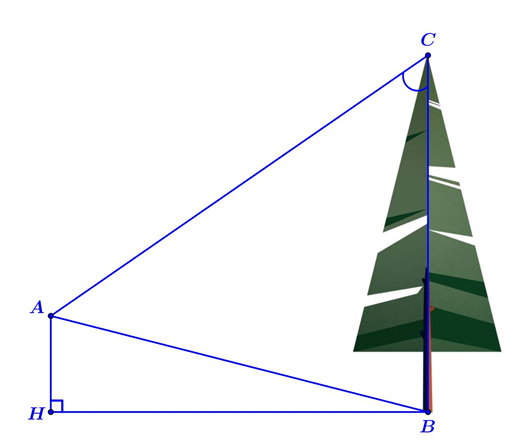 Biết \[AH = 4{\rm{m}}\], \[HB = 20{\rm{m}}\], \[\widehat {BAC} = {45^^\circ }\]. Khi đó chiều cao của cây (làm tròn đến hàng phần mười) bằng
Biết \[AH = 4{\rm{m}}\], \[HB = 20{\rm{m}}\], \[\widehat {BAC} = {45^^\circ }\]. Khi đó chiều cao của cây (làm tròn đến hàng phần mười) bằng