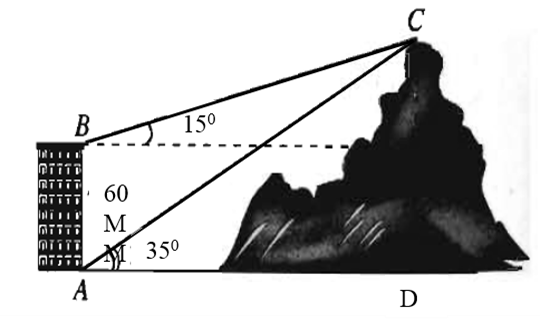
Từ hai vị trí \[A,\,\,B\] của một tòa nhà, người ta quan sát đỉnh \[C\] của một ngọn núi. Biết rằng \[A\] là điểm nằm phía chân của tòa nhà tiếp xúc với mặt đất, \[B\] là điểm nằm trên nóc của tòa nhà, phương \[A\,B\] vuông góc với mặt đất, khoảng cách \[A\,B\] là 70\[(m)\], phương nhìn \[AC\] tạo với phương nằm ngang một góc \[30^\circ \], phương nhìn \[BC\] tạo với phương nằm ngang một góc \[15^\circ 30'\]. Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất (làm tròn đến hàng phần trăm)?

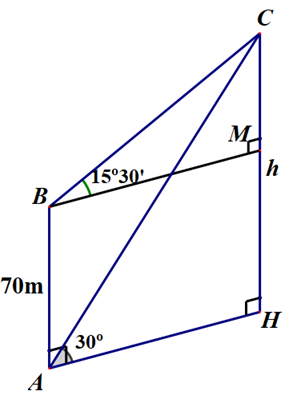
Gọi \[H\] là hình chiếu của \[C\] trên mặt đất, \[M\] là hình chiếu của \[B\] trên \[CH\]. Chiều cao của ngọn núi là \[h = CH\]. Xét điều kiện trong thực tế đỉnh núi cao hơn nóc tòa nhà thì \[h > 70\] và \[M\] nằm giữa hai điểm \[C\] và \[H\].

\[\Delta ACH\] vuông tại \[H,{\rm{ }}\widehat {CAH} = 30^\circ  \Rightarrow h = AH.\tan 30^\circ \] (1)

\[\Delta BCM\] vuông tại \[M,{\rm{ }}\widehat {CBM} = 15^\circ 30' \Rightarrow CM = BM.\tan \left( {15^\circ 30'} \right) = AH.\tan \left( {15^\circ 30'} \right)\]

\[ \Rightarrow AH = \frac{{h - 70}}{{\tan \left( {15^\circ 30'} \right)}}{\rm{ }}\left( 2 \right)\]

Từ (1) và (2) suy ra \[h = \frac{{h - 70}}{{\tan \left( {15^\circ 30'} \right)}}.\tan 30^\circ  \Leftrightarrow h = \frac{{70.\tan 30^\circ }}{{\tan 30^\circ  - \tan \left( {15^\circ 30'} \right)}} \approx 134,70(m)\].