PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
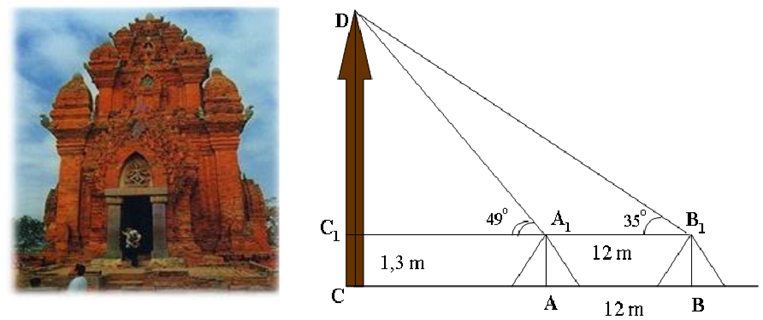
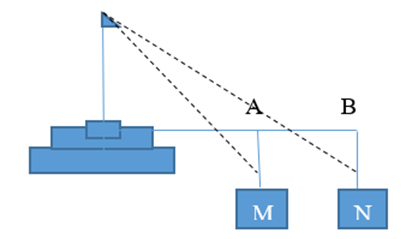
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một Kỳ đài trước Ngọ Môn ( Đại Nội – Huế). Người ta cắm hai cọc bằng nhau MA và NB cao 1,5 mét so với mặt đất. Hai cọc này song song. cách nhau 10 mét và thẳng hàng so với cột cờ ( xem hình vẽ minh họa ). Đặt giác kế đứng tại A và B để nhắm đến đỉnh cột cờ, người ta đo được các góc lần lượt là \({52^ \circ }45'\) và \({45^ \circ }50'\) so với đường thẳng song song với mặt đất. Hãy tính chiều cao của cột cờ ( làm tròn đến 0,01 m).
PHẦN IV. Câu hỏi tự luận.Thí sinh trình bày lời giải vào giấy làm bài.
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một Kỳ đài trước Ngọ Môn ( Đại Nội – Huế). Người ta cắm hai cọc bằng nhau MA và NB cao 1,5 mét so với mặt đất. Hai cọc này song song. cách nhau 10 mét và thẳng hàng so với cột cờ ( xem hình vẽ minh họa ). Đặt giác kế đứng tại A và B để nhắm đến đỉnh cột cờ, người ta đo được các góc lần lượt là \({52^ \circ }45'\) và \({45^ \circ }50'\) so với đường thẳng song song với mặt đất. Hãy tính chiều cao của cột cờ ( làm tròn đến 0,01 m).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 10 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
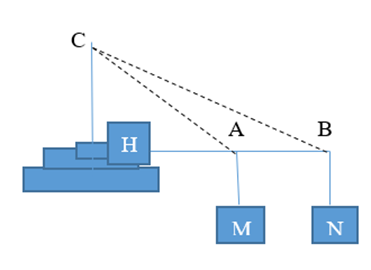
Gọi H là chân đường vuông góc từ AB đến cột cờ.
Xét tam giác ABC ta có: \(\widehat {ACB} = \widehat {CAH} - \widehat {ABC} = {52^ \circ }45' - {45^ \circ }50' = {6^ \circ }55'\)
Theo định lí Sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin (\widehat {ACB})}} = \frac{{AC}}{{\sin (\widehat B)}} \Rightarrow AC = \frac{{AB.\sin (\widehat B)}}{{\sin (\widehat {ACB})}} = 35,74(m)\).
Xét tam giác ACH vuông tại H ta có \(CH = AC.\sin \widehat {CAH} = 28,45(m)\).
Vậy chiều cao của cột cờ là 28,45 mét.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Trả lời |
4 |
5 |
|
|
Gọi \(x,y\) lần lượt là diện tích (ha) trồng nha đam và măng tây \(\left( {x \ge 0,\,y \ge 0} \right)\).
Theo bài ta có hệ phương trình sau: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 10\\10x + 30y \le 150\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 10\\x + 3y \le 15\end{array} \right.\)
Số tiền người nông dân thu được là: \(F(x,y) = 4x + 6y\) (triệu).
Ta cần tìm giá trị lớn nhất của hàm \(F(x,y) = 4x + 6y\) với \(x,y\) thỏa mãn các điều kiện trong đề bài.
Bước 1. Biểu diễn miền nghiệm và xác định miền nghiệm của hệ bất phương trình trên.
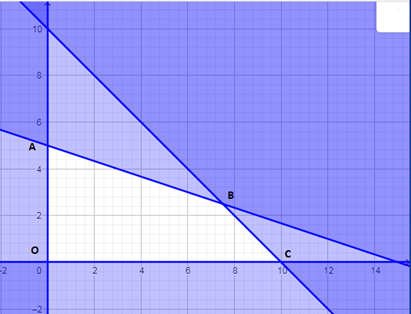
Miền nghiệm là tứ giác \(OABC\) với tọa độ các đỉnh \(O(0;0)\),\(A(0;5)\),\(B(7,5;\,2,5)\),\(C(10,0)\),.
Bước 2. Tính giá trị của biểu thức \(F\) tại các đỉnh của ngũ giác này:
\(F(0,0) = 0\),\(F(0;5) = 30\),\(F(7,5;\,2,5) = 30 + 15 = 45\),\(F(10;0) = 40\).
Bước 3. So sánh các giá trị thu được của \(F\) ở Bước 2, ta được giá trị lớn nhất cần tìm là: \(F(7,5;\,2,5) = 30 + 15 = 45\).
Vậy số tiền bác nông dân thu được nhiều nhất là \(45\) triệu.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Trả lời |
3 |
0 |
|
|
Gọi \(x\) là số học sinh chỉ biết chơi 2 môn thể thao bóng đá và bóng bàn, \(y\) là số học sinh chỉ biết chơi 2 môn thể thao bóng bàn và bóng rổ, \(z\) là số học sinh chỉ biết chơi 2 môn thể thao bóng rổ và bóng đá.
Ta có : \(\left\{ \begin{array}{l}x + n\left( {A \cap B \cap C} \right) = n\left( {A \cap B} \right)\\y + n\left( {A \cap B \cap C} \right) = n\left( {B \cap C} \right)\\z + n\left( {A \cap B \cap C} \right) = n\left( {A \cap C} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 5 = 15\\y + 5 = 20\\z + 5 = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = 15\\z = 5\end{array} \right.\).
Số học sinh chỉ biết chơi đúng 2 môn thể thao trong 3 môn thao bóng đá, bóng bàn và bóng rổ là 30 em.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
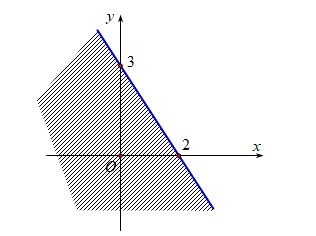
A. \[2x + 3y \ge 6\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập