Giải hệ phương trình: \[\left\{ \begin{array}{l}\frac{3}{{x + 1}} - 2y =  - 1\\\frac{5}{{x + 1}} + 3y = 11\end{array} \right.\]

Một thùng nước có dạng hình trụ với chiều cao \[1,6m\] và bán kính đáy \[0,5m.\] Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này (trừ hai mặt đáy). Tính diện tích bề mặt được sơn của thùng nước (lấy \[\pi  \approx 3,14\]).

Cho tam giác \[ABC\] vuông tại \[A\]. Vẽ đường tròn tâm \[C\], bán kính \[CA\]. Từ điểm \[B\] kẻ tiếp tuyến \[BM\] với đường tròn \[(C\,;\,CA)\] (\[M\] là tiếp điểm, \[M\] và \[A\] nằm khác phía đối với đường thẳng \[BC\]).

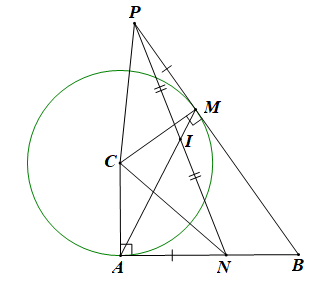
1) Chứng minh bốn điểm \[A\,,\,C\,,\,M\,\] và \(B\) cùng thuộc một đường tròn.

2) Lấy điểm \[N\] thuộc đoạn thẳng \[AB\] (\[N\] khác \[A\], \[N\] khác \[B\]). Lấy điểm \[P\] thuộc tia đối của tia \[MB\] sao cho \[MP = AN\]. Chứng minh tam giác \[CPN\] là tam giác cân và đường thẳng \[AM\] đi qua trung điểm của đoạn thẳng \[NP\].

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Một tổ sản xuất phải làm xong \[4800\] bộ đồ bảo hộ y tế trong một số ngày quy định. Thực tế, mỗi ngày tổ đó làm được nhiều hơn \[100\] bộ đồ bảo hộ y tế so với số bộ đồ bảo hộ y tế phải làm trong một ngày theo kế hoạch. Vì thế \[8\] ngày trước khi hết hạn, tổ sản xuất đã làm xong \[4800\] bộ đồ bảo hộ y tế đó. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu bộ đồ bảo hộ y tế? (Giả định rằng số bộ đồ bảo hộ y tế mà tổ đó làm xong trong mỗi ngày là bằng nhau.)

Trong mặt phẳng tọa độ \[Oxy\], cho parabol \[(P):\,y = {x^2}\] và đường thẳng \[(d):\,y = 2x + m - 2\]. Tìm tất cả giá trị của \[m\] để \[(d)\] cắt \[(P)\] tại hai điểm phân biệt có hoành độ \[{x_1}\,,\,{x_2}\] sao cho \[\left| {{x_1} - {x_2}} \right| = 2\].

Cho hai biểu thức \[A = \frac{{\sqrt x }}{{\sqrt x  + 3}}\] và \[B = \frac{{2\sqrt x }}{{\sqrt x  - 3}} - \frac{{3x + 9}}{{x - 9}}\] với \[x \ge 0,x \ne 9.\]

1) Tính giá trị của biểu thức \[A\] khi \[x = 16.\]

2) Chứng minh \[A + B = \frac{3}{{\sqrt x  + 3}}.\]

Với các số thực \[a\] và \[b\] thỏa mãn \[{a^2} + {b^2} = 2\], tìm giá trị nhỏ nhất của biểu thức \[P = 3(a + b) + ab\].