Cho tam giác \[ABC\] nhọn có \[AB < AC\] và nội tiếp trong đường tròn tâm \[O\] đường kính \[AD\]. Gọi \[AH\] là đường cao của tam giác \[ABC\]. Qua \[B\] kẻ đường thẳng vuông góc với đường thẳng \[AD\] tại \[E\].
a) Chứng minh \[ABHE\] là tứ giác nội tiếp.
b) Chứng minh hai đường thẳng \[HE\] và \[AC\] vuông góc với nhau.
c) Gọi \[F\] là hình chiếu vuông góc của điểm \[C\] lên đường thẳng \[AD\] và \[M\] là trung điểm của đoạn thẳng \[BC\]. Chứng minh rằng \[M\] là tâm đường tròn ngoại tiếp tam giác \[HEF\].
Cho tam giác \[ABC\] nhọn có \[AB < AC\] và nội tiếp trong đường tròn tâm \[O\] đường kính \[AD\]. Gọi \[AH\] là đường cao của tam giác \[ABC\]. Qua \[B\] kẻ đường thẳng vuông góc với đường thẳng \[AD\] tại \[E\].
a) Chứng minh \[ABHE\] là tứ giác nội tiếp.
b) Chứng minh hai đường thẳng \[HE\] và \[AC\] vuông góc với nhau.
c) Gọi \[F\] là hình chiếu vuông góc của điểm \[C\] lên đường thẳng \[AD\] và \[M\] là trung điểm của đoạn thẳng \[BC\]. Chứng minh rằng \[M\] là tâm đường tròn ngoại tiếp tam giác \[HEF\].
Quảng cáo
Trả lời:
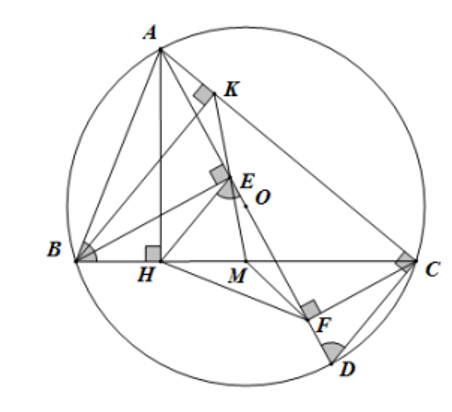
a) Vì \[AH \bot BC,\,\,BE \bot AD\] nên \[\widehat {AHB} = \widehat {AEB} = 90^\circ \].
Suy ra tứ giác \[ABHE\] là tứ giác nội tiếp.
b) Vì \[\widehat {ACD}\] là góc nội tiếp chắn nửa đường tròn nên \[\widehat {ACD} = 90^\circ \Rightarrow AC \bot CD\]. (1)
Vì \[ABHE\] là tứ giác nội tiếp nên \[\widehat {ABH} = \widehat {HED}\] (góc trong và góc ngoài đỉnh đối diện).
Vì \[ABDC\] là tứ giác nội tiếp đường tròn \[\left( O \right)\] nên \[\widehat {ABC} = \widehat {ADC}\] (2 góc nội tiếp cùng chắn cung \[\widehat {ABC} = \widehat {ADC}\]), hay \[\widehat {ABH} = \widehat {EDC}\].
Suy ra \[\widehat {HED} = \widehat {EDC} \Rightarrow EH{\rm{//}}DC\]. (2)
Từ (1) và (2) suy ra \[HE \bot AC\].
c) Vẽ \[BK \bot AC\] tại \[K\].
Ta có \[\widehat {AKB} = \widehat {AEB} = 90^\circ \] nên \[AKEB\] là tứ giác nội tiếp.
Suy ra \[\widehat {BKE} = \widehat {BAE} = \widehat {BAD}\] (2 góc nội tiếp cùng chắn cung \[BE\]). (3)
Vì \[ABDC\] là tứ giác nội tiếp nên \[\widehat {BAD} = \widehat {BCD}\] (2 góc nội tiếp cùng chắn cung \[BD\]). (4)
Vì \[BK\,{\rm{//}}\,CD\] (cùng vuông góc \[AC\]) nên \[\widehat {BCD} = \widehat {KBM}\] (so le trong). (5)
Vì \[M\] là trung điểm cạnh huyền \[BC\] của tam giác vuông \[BKC\] nên \[MK = MB = MC\].
Suy ra \[\Delta MKB\] cân tại \[M\] \[ \Rightarrow \widehat {KBM} = \widehat {BKM}\]. (6)
Từ (3), (4), (5), (6) có \[\widehat {BKE} = \widehat {BKM}\] \[ \Rightarrow K,\,E,\,M\] thẳng hàng.
Mà \[HE\,{\rm{//}}BK\] (cùng vuông góc \[AC\]) nên \[\frac{{ME}}{{MH}} = \frac{{MK}}{{MB}} = 1\]\[ \Rightarrow ME = MH\].
Chứng minh tương tự ta có \[MF = MH\].
Suy ra \[ME = MF = MH\]
Vậy\[M\] là tâm đường tròn ngoại tiếp tam giác \[HEF\] (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chiều dài của hình chữ nhật đó là \[x\] (cm) (\[x > 4\]).
Vì chiều rộng bằng \[\frac{3}{5}\] chiều dài nên chiều rộng của hình chữ nhật là \[\frac{3}{5}x\] (cm).
Diện tích của hình chữ nhật ban đầu là \[\frac{3}{5}{x^2}\] (cm2).
Khi giảm chiều rộng 1 cm và giảm chiều dài 4 cm thì diện tích của hình chữ nhật mới là \[\left( {\frac{3}{5}x - 1} \right)\left( {x - 4} \right)\,\,\,\,{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\]
Diện tích hình chữ nhật mới bằng một nửa diện tích ban đầu nên ta có phương trình:
\[\left( {\frac{3}{5}x - 1} \right)\left( {x - 4} \right) = \frac{1}{2}.\frac{3}{5}{x^2}\]
\[ \Leftrightarrow \frac{3}{{10}}{x^2} - \frac{{17}}{5}x + 4 = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = 10\,\,\,\,\,(TM)\\x = \frac{4}{3}\,\,\,\,(L)\end{array} \right.\]
Chiều dài và chiều rộng của hình chữ nhật ban đầu lần lượt là 10 cm và \[\frac{3}{5}\].10 = 6 cm.
Chu vi miếng bìa là 2 . (10 + 6) = 32 (cm).
Lời giải
a) \[y = \frac{1}{2}{x^2}\]
Bảng giá trị
|
\[x\] |
– 2 |
– 1 |
0 |
1 |
2 |
|
\[y\] |
2 |
\[\frac{1}{2}\] |
0 |
\[\frac{1}{2}\] |
2 |
Đồ thị hàm số \[y = \frac{1}{2}{x^2}\] là đường cong đi qua các điểm \[\left( { - 2;\,2} \right),\,\left( { - 1;\,\frac{1}{2}} \right),\,\left( {0;0} \right),\,\left( {1;\,\frac{1}{2}} \right),\,\left( {2;\,2} \right)\]
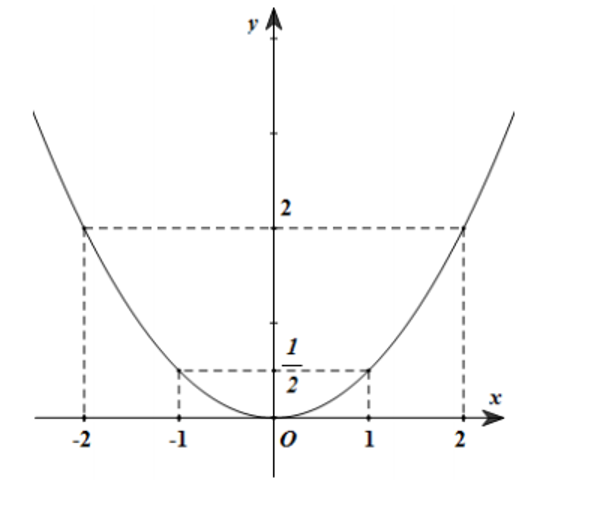
b)
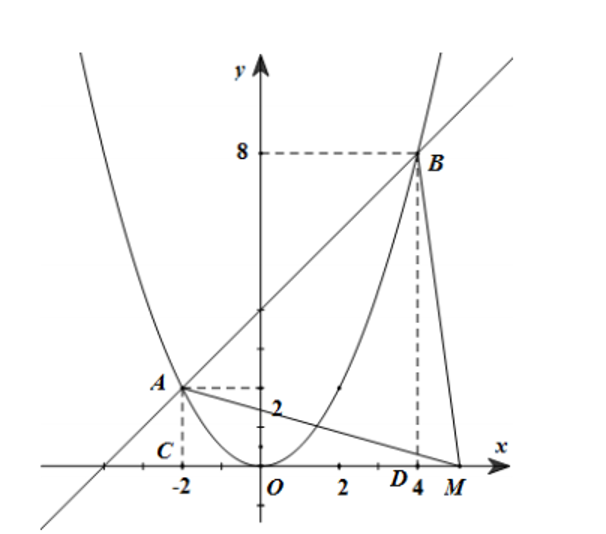
Xét phương trình hoành độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\] là:
\[\frac{1}{2}{x^2} = x + 4 \Leftrightarrow {x^2} - 2x - 8 = 0\]
Ta có: \[\Delta ' = {\left( { - 1} \right)^2} - \left( { - 8} \right) = 9 > 0\]
Do đó, phương trình có 2 nghiệm phân biệt: \[x = 4;\,x = - 2\].
Với \[x = - 2\] ta có \[y = 2 \Rightarrow A\left( { - 2;\,2} \right)\]
Với \[x = 4\] ta có \[y = 8 \Rightarrow B\left( {4;\,8} \right)\].
Gọi \[M\left( {m;\,\,0} \right)\] thuộc tia \[Ox\left( {m > 0} \right)\]. Gọi \[C\left( { - 2;\,0} \right),\,D\left( {4;\,0} \right)\]. Xét hai trường hợp:
+ Trường hợp 1: \[M\] thuộc đoạn \[OD\]. Ta có \[{S_{AMB}} = {S_{ABDC}} - {S_{ACM}} - {S_{BDM}}\]
Có \[ABDC\] là hình thang có \[AC\] = 2 cm, \[BD\] = 8 cm, \[CD\] = 6 cm.
\[ \Rightarrow {S_{ABDC}} = \frac{{\left( {2 + 8} \right).6}}{2} = 30\,\,(c{m^2})\]
Suy ra \[{S_{AMB}}\] < 30 cm2 (loại).
+ Trường hợp 2: \[M\] thuộc tia \[Dx\,\,\left( {M \ne D} \right) \Rightarrow m > 4\].
Ta có :\[{S_{AMB}} = {S_{ABDC}} - {S_{ACM}} + {S_{BDM}}\]
Có \[{S_{ABDC}}\] = 30 cm2, \[MC = m + 2\] (cm), \[MD = m - 4\] (cm)
Suy ra
\[{S_{ACM}} = \frac{1}{2}AC.CM = \frac{1}{2}.2.\left( {m + 2} \right) = m + 2\,\,\,({\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\]
\[{S_{BDM}} = \frac{1}{2}BD.DM = \frac{1}{2}.8.\left( {m - 4} \right) = 4\left( {m - 4} \right)\,\,{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\]
\[ \Rightarrow {S_{AMB}} = 30c{m^2} \Leftrightarrow {S_{ACM}} = {S_{BDM}} \Leftrightarrow m + 2 = 4\left( {m - 4} \right) \Leftrightarrow m = 6\] (thỏa mãn).
Vậy \[M\left( {6;\,0} \right)\] là điểm cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.