Một hộp có 12 viên bi, trong đó có 7 viên bi xanh và 5 viên bi đỏ. Chọn ngẫu nhiên 5 viên bi trong hộp. Hãy xác định định đúng – sai của các khẳng định sau:
a) Số phần tử của không gian mẫu là 792.
b) Xác suất của biến cố \[A\]: “ 5 viên bi đều là mầu xanh” là \[\frac{7}{{264}}\].
c) Xác suất của biến cố \[B\]: “ Trong \[5\] viên bi lấy được có 3 bi xanh và 2 bi đỏ” là \[\frac{{125}}{{462}}\]
d) Xác suất của biến cố \[C\]: “ Trong 5 viên bi lấy được có ít nhất 3 bi đỏ” là \[\frac{{125}}{{396}}\].
Quảng cáo
Trả lời:
a) Đúng: Không gian mẫu là tập tất cả các tập con gồm 5 viên bi từ 12 viên bi. Vậy số phần tử của không gian mẫu là \[n\left( \Omega \right) = C_{12}^5 = 792\].
b) Đúng: Chọn 5 bi xanh từ 7 bi xanh, có \[C_7^3 = 21\] (cách chọn) \[ \Rightarrow n\left( A \right) = 21\].
Vậy xác suất của biến cố \[A\] là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{21}}{{792}} = \frac{7}{{264}}\].
c) Sai: Mỗi phần tử của \[B\] được hình thành từ 2 bước:
Bước 1: Chọn 3 viên bi xanh từ 7 viên bi xanh, có \[C_7^3 = 35\] (cách chọn).
Bước 2: Chọn 2 viên bi đỏ từ 5 viên bi đỏ, có \[C_5^2 = 10\] (cách chọn).
Theo quy tắc nhân, tập \[B\] có \[35.10 = 350\] (phần tử). Vậy \[n\left( B \right) = 350 \Rightarrow P\left( B \right) = \frac{{350}}{{792}} = \frac{{175}}{{396}}\].
d) Đúng: Trong 5 viên bi lấy được có ít nhất 3 bi đỏ, có 3 cách:
Cách 1: Trong \[5\] viên bi được chọn có 2 bi xanh và 3 bi đỏ: có \[\mathop C\nolimits_7^2 .\mathop C\nolimits_5^3 = 210\] (cách chọn)
Cách 2: Trong \[5\] viên bi được chọn có 1 bi xanh và 4 bi đỏ: có \[C_7^1.C_5^4 = 35\] (cách chọn).
Cách 3: Trong \[5\] viên bi được chọn có 0 bi xanh và 5 bi đỏ: có \[C_7^0.C_5^5 = 5\] (cách chọn).
Theo quy tắc cộng, tập \[C\] có \[210 + 35 + 5 = 250\] (phần tử).
Vậy \[n\left( C \right) = 250 \Rightarrow P\left( C \right) = \frac{{250}}{{792}} = \frac{{125}}{{396}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
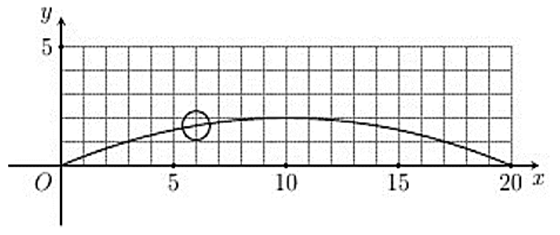
Yêu cầu bài toán \( \Leftrightarrow - 0,02{x^2} + 0,4x \ge 1,5\)\( \Leftrightarrow 5 \le x \le 15\).
Vậy quả bóng đạt độ cao lớn hơn hay bằng \(1,5\) mét trong khoảng \(15 - 5 = 10\) ( giây).
Lời giải
a) Đúng: Gọi số cần tìm có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}} \) trong đó \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6};{a_7} \in S\)
Chọn \({a_1}({a_1} \ne 0)\): có \(6\) cách chọn
Ta có: \({a_2};{a_3};{a_4};{a_5};{a_6};{a_7}\) có số cách chọn là số hoán vị của 6 phần tử: \(6!\)
Vậy có \(6.6!\) số
b) Sai: Gọi số cần tìm có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}} \) trong đó \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6};{a_7} \in S\)
TH1: Chọn \({a_1};{a_2};{a_3} \in \left\{ {1;2;3} \right\}\),\(({a_1} \ne 0)\)có \(3!\) cách chọn
Chọn \({a_4};{a_5};{a_6};{a_7}\) có số cách chọn là số hoán vị của 4 phần tử còn lại: \(4!\) cách chọn
Do vậy ta được \(3!\).\(4!\)=144 số
TH2: Các số \(1;2;3\) nằm ở ba trong 4 vị trí \({a_4};{a_5};{a_6};{a_7}\) có: \(4.3.2 = 24\) cách sắp xếp
Chọn \({a_1} \in \left\{ {4;5;6} \right\}\) có: 3 cách chọn
Còn 3 vị trí còn lại có số cách chọn là số hoán vị của 3 phần tử còn lại từ tập \(S\): \(3!\) cách chọn
Do vậy ta có: \(24.3.3! = 432\) số
Tổng cộng có 576 số
c) Đúng: Gọi số cần tìm có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \) trong đó \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6} \in S\backslash \left\{ 0 \right\}\)
Ta có: \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\) có số cách chọn là số hoán vị của 6 phần tử: \(6!\)
Do vậy ta có \(6!\) số
d) Sai: Gọi số cần tìm có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}} \) trong đó \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6};{a_7} \in S\)
TH1: Chọn \({a_7} = 0\): có 1 cách chọn
Chọn \({a_1};{a_2};{a_3};{a_4};{a_5};{a_6}\) có số cách chọn là số hoán vị của 6 phần tử: \(6!\)
Do vậy ta có \(6!\) số
TH2: Chọn \({a_7} \in \left\{ {2,4,6} \right\}\): có 3 cách chọn
Chọn \({a_1}({a_1} \ne 0;\,{a_1} \ne {a_7})\): có 5 cách chọn
Chọn \({a_2};{a_3};{a_4};{a_5};{a_6}\) có số cách chọn là số hoán vị của 5 phần tử: \(5!\)
Do vậy ta có: \(3.5.5!\) số
Vậy tổng có: \(6! + 3.5.5!\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.