Quảng cáo
Trả lời:
Giải bởi Vietjack
Giải phương trình: \((3x - 5)(2x + 4) = 0\)
\((3x - 5)(2x + 4) = 0\)
\(3x - 5 = 0\) hoặc \(2x + 4 = 0\)
\(x = \frac{5}{3}\) hoặc \(x = - 2\)
Câu hỏi cùng đoạn
Câu 2:
Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y = 2}\\{2x + y = 5}\end{array}} \right.\)
Giải bởi Vietjack
Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y = 2}\\{2x + y = 5}\end{array}} \right.\)
Từ phương trình thứ hai: \(y = 5 - 2x\)
Thay vào phương trình thứ nhất:
\(3x - 4(5 - 2x) = 2\)
\(3x - 20 + 8x = 2\)
\(11x = 22 \Rightarrow x = 2\)
Thay \(x = 2\) vào \(y = 5 - 2x\):
\(y = 5 - 4 = 1\)
Vậy nghiệm hệ: \((x,y) = (2;1)\)
Câu 3:
Hai xe ô tô xuất phát cùng một lúc từ Thánh phố Đồng Xoài đến Thành phố Hồ Chí Minh dài 90 km. Biết vận tốc xe thứ hai hơn vận tốc xe thứ nhất 15 km/h nên xe thứ hai đến Thành phố Hồ Chí Minh sớm hơn xe thứ nhất 30 phút. Tính vận tốc của mỗi xe.
Giải bởi Vietjack
Đổi 30 phút = \(\frac{1}{2}\) (h)
Gọi vận tốc của xe ô tô thứ nhất là \(x\) (km/h), với \(x > 0\).
Vận tốc xe ô tô thứ hai là \(x + 15\) (km/h).
Thời gian xe ô tô thứ nhất và thứ hai đi hết quãng đường lần lượt là: \(\frac{{90}}{x}\quad (h)\)
Thời gian xe ô tô thứ hai đi hết quãng đường lần lượt là: \(\frac{{90}}{{x + 15}}\quad (h)\)
Theo bài, ta có phương trình: \(\frac{{90}}{x} - \frac{{90}}{{x + 15}} = \frac{1}{2}\)
\(\begin{array}{l}\frac{{90\,.\,2\left( {x + 15} \right)}}{{2x\left( {x + 15} \right)}} - \frac{{90\,.\,2x}}{{2x(x + 15)}} = \frac{{x(x + 15)}}{{2x(x + 15)}}\\\end{array}\)
\(180x + 2700 - 180x = {x^2} + 15x\)
\({x^2} + 15x - 2700 = 0\)
Giải phương trình ta được \(x = 45\) (loại nghiệm \(x = - 60\)).
Vậy vận tốc xe thứ nhất là \(45\) km/h, vận tốc xe thứ hai là \(45 + 15 = 60\) km/h.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
(2,0 điểm)
Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \((O)\). Các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\).
a) Chứng minh tứ giác \(BCDE\) nội tiếp đường tròn.
b) Chứng minh \(AE\,.\,AB = AD\,.\,AC\)
c) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(AH\). Gọi \(K,\,\,L\)lần lượt là giao điểm của hai đường thẳng \(OM\) và \(CE\), \(MN\) và \(BD\).
Chứng minh \(\widehat {MLB}\,\, = \,\,\widehat {MKB}\)
(2,0 điểm)
Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \((O)\). Các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\).
a) Chứng minh tứ giác \(BCDE\) nội tiếp đường tròn.
b) Chứng minh \(AE\,.\,AB = AD\,.\,AC\)
c) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(AH\). Gọi \(K,\,\,L\)lần lượt là giao điểm của hai đường thẳng \(OM\) và \(CE\), \(MN\) và \(BD\).
Chứng minh \(\widehat {MLB}\,\, = \,\,\widehat {MKB}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
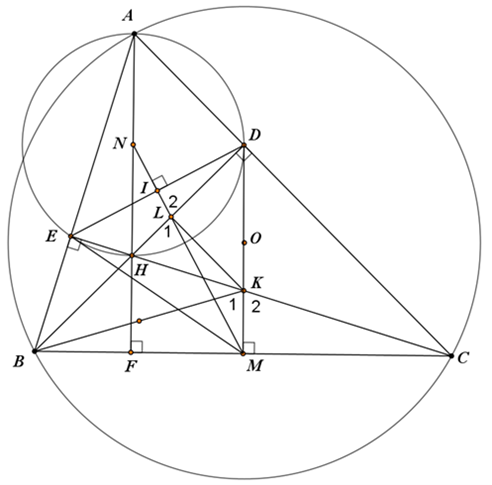
a) Chứng minh tứ giác \(BCDE\) nội tiếp đường tròn.
Ta có: \(\Delta BCE\) vuông tại \(E\) nên nội tiếp đường tròn đường kính \(BC\).
\(\Delta BCD\) vuông tại \(D\) nên nội tiếp đường tròn đường kính \(BC\).
Suy ra tứ giác \(BCDE\) nội tiếp đường tròn đường kính \(BC\).
b) Chứng minh \(AE\,.\,AB = AD\,.\,AC\)
+) Xét hai \(\Delta AED\) và \(\Delta ACB\):
- Vì tứ giác \(BCDE\) nội tiếp nên\(\widehat {BED} + \widehat {BCD} = {180^O}\)
- Lại có \(\widehat {BED} + \widehat {DEA} = 180^\circ \) (hai góc kề bù).
Suy ra \(\widehat {BCD} = \widehat {DEA}\); \(\widehat {BAC}\) chung
+) nên
Suy ra: \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} \Rightarrow AE.AB = AD.AC\)
Cách 2: Xét hai tam giác vuông \(\Delta ADB\) và \(\Delta AEC\):
Có \(\widehat {BAC}\) chung nên (góc nhọn).
c) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(AH\). Gọi \(K,\,\,L\)lần lượt là giao điểm của hai đường thẳng \(OM\) và \(CE\), \(MN\) và \(BD\).
Chứng minh \(\widehat {MLB}\,\, = \,\,\widehat {MKB}\)
+) Gọi \(I\) là giao điểm của \(ED\) và \(MN\) suy ra \(MN\) là trung trực của \(ED\) (do \(MD = ME\) và \(ND = NE\)).
+) Xét \(\Delta IDL\) và \(\Delta MCK\) có: \(\widehat {IDL} = \widehat {EDH} = \widehat {ECB}\).
Nên
Suy ra \({\widehat K_2} = {\widehat L_2}\). Mà \({\widehat K_1} = {\widehat K_2}\) và \({\widehat L_1} = {\widehat L_2}\).
Do đó \({\widehat K_1} = {\widehat L_1}\).
Vậy: \(\widehat {MLB} = \widehat {MKB}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Hãy lập bảng tần số và bảng tần số tương đối số điểm của học sinh.
|
Điểm kiểm tra CK2 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số |
2 |
3 |
4 |
7 |
14 |
10 |
|
Tần số tương đối |
5% |
7,5% |
10% |
17,5% |
35% |
25% |
b) Lấy ngẫu nhiên một học sinh, tính xác suất để học sinh này có số điểm lớn hơn 8.
Không gian mẫu lấy 1 học sinh trong 40 học sinh là \[n(\Omega ) = 40\]
Gọi A là “Lấy 1 học sinh có điểm số lớn hơn 8” . Do đó \[n(A) = 24\]
Xác xuất của biến cố A là : \[P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{24}}{{40}} = \frac{3}{5} = 0,6\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập