Câu hỏi:

10/01/2026 31

Giải hệ phương trình sau:

\[\left\{ {\begin{array}{*{20}{l}}{{x^3} - 2y + x - 2{x^2}y = 0}\\{\sqrt {x + 1} - \sqrt {16 - y} = 3}\end{array}} \right.\]

Xem lời giải

Câu hỏi trong đề: Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 sở GD&ĐT Kiên Giang có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Điều kiện: $x \ge - 1$ và $y \le 16$. (1)

Với điều kiện đó, ta có:

$\left\{ {\begin{array}{*{20}{l}}{{x^3} - 2y + x - 2{x^2}y = 0}\\{\sqrt {x + 1} - \sqrt {16 - y} = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{(x - 2y)\left( {{x^2} + 1} \right) = 0}\\{\sqrt {x + 1} - \sqrt {16 - y} = 3}\end{array}} \right.} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2y}\\{\sqrt {2y + 1} - \sqrt {16 - y} = 3.}\end{array}} \right.$

Ta có:

$\begin{array}{l}{\rm{ (3) }} \Leftrightarrow (\sqrt {2y + 1} - 5) - (\sqrt {16 - y} - 2) = 0\\ \Leftrightarrow \frac{{2(y - 12)}}{{\sqrt {2y + 1} + 5}} + \frac{{y - 12}}{{\sqrt {16 - y} + 2}} = 0\\ \Leftrightarrow (y - 12)\left( {\frac{2}{{\sqrt {2y + 1} + 5}} + \frac{1}{{\sqrt {16 - y} + 2}}} \right) = 0\\ \Leftrightarrow y = 12.\end{array}$

Thay $y = 12$ vào (2), ta được $x = 24$.

Cặp số $\left( {x,y} \right) = \left( {24,12} \right)$ thỏa mãn (1). Vì thế, cặp số đó là nghiệm duy nhất của hệ phương trình đã cho.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vuông $ABCD$ có cạnh bằng 8. Trên cạnh $BC$, lấy điểm $M$ sao cho $BM = 5$. Gọi $N$ là giao điểm của đường thẳng $CD$ và đường thẳng vuông góc với $AM$ tại $A$. Gọi $I$ là trung điểm của $MN$. Hãy tính độ dài đoạn thẳng $DI$.

Xem đáp án

Lời giải

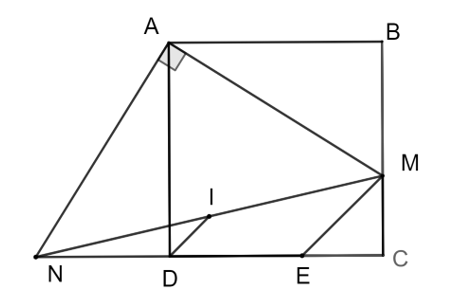
$Cho hình vuông $ABCD$ có cạnh bằng 8. Trên cạnh $BC$, lấy điểm $M$ sao cho (ảnh 1)$

Xét hai tam giác vuông $ABM$ và $ADN$, ta có:

$AB = AD$,$\widehat {BAM} = \widehat {DAN}$ (hai góc nhọn có cạnh tương ứng vuông góc)

Do đó tam giác $\Delta ABM = \Delta ADN$ (cạnh góc vuông – góc nhọn). Suy ra, $DN = BM$ (1).

Qua $M$ kẻ đường thẳng song song $ID$ cắt $NC$ tại \[E\].

Xét tam giác $MNE$:

Do $I$ là trung điểm của $MN$ và $ID\,{\rm{//}}\,ME$, nên $D$ là trung điểm của $NE$. Vì thế $DE = DN = BM$ (theo (1)). Suy ra, $MC = CE$ (2)

Do $I,D$ tương ứng là trung điểm của $MN,\,NE$, nên $ID$ là đường trung bình của tam giác. Do đó, $DI = \frac{1}{2}EM$.

Xét tam giác vuông (tại C) MCE, theo định lí Pitago, ta có:

$EM = \sqrt {M{C^2} + C{E^2}} = \sqrt {2M{C^2}} $(do (2))

$ = \sqrt 2 MC = \sqrt 2 \left( {BC - BM} \right) = \sqrt 2 \left( {8 - 5} \right) = 3\sqrt 2 $.

Vì thế $DI = \frac{{3\sqrt 2 }}{2}$.

Câu 2

a) Cho $m,\,p,\,r$ là các số nguyên tố thỏa mãn $mp + 1 = r$. Chứng minh rằng ${m^2} + r$ hoặc ${p^2} + r$ là số chính phương.

b) Tìm tất cả các số nguyên tố $q$, sao cho tồn tại số nguyên dương $n$ để ${n^2} + 22q$ là một lũy thừa với số mũ nguyên dương của 11.

Xem đáp án

Lời giải

a)Vì $m,\,p$ là các số nguyên tố nên $mp \ge 4$. Do đó, $r \ge 5$. Mà $r$ là nguyên tố nên r là số lẻ.

Vì thế, $mp = r - 1$ là một số chẵn. Suy ra, trong hai số $m,\,p$, có ít nhất một số bằng 2.

- Nếu $m = 2$ thì $r = 2p + 1$. Do đó:

${p^2} + r = {p^2} + 2p + 1 = {\left( {p + 1} \right)^2}$,

Là một số chính phương.

- Nếu $p = 2$ thì $r = 2m + 1$. Do đó

${m^2} + r = {m^2} + 2m + 1 = {\left( {m + 1} \right)^2}$ là một số chính phương

b)Giả sử q là số nguyên tố thỏa mãn yêu cầu đề bài. Khi đó, sẽ tồn tại các số nguyên dương

\[n,\,k\] sao cho ${n^2} + 22q = {11^k}$. (1)

Do ${n^2} + 22q > 11$ nên ${11^k} > 11$; suy ra $k \ge 2$. Vì thế, từ (1), ta có:

$\left( {{n^2} + 22q} \right) \vdots {11^2}$. (2)

Do $22q \vdots 11$ nên từ (1) suy ra, ${n^2} \vdots 11$; mà 11 là số nguyên tố, nên ${n^2} \vdots {11^2}$. (3)

Từ (2) và (3) suy ra, $22q \vdots {11^2}$. Do đó, \[q \vdots 11\]; mà \[q\] là số nguyên tố nên $q = 11$.

Ngược lại, với $q = 11$, ta có: ${33^2} + 22.11 = {11^2}.\left( {9 + 2} \right) = {11^3}$.

Vậy có duy nhất số q thỏa yêu cầu của đề bài là $q = 11$.

Câu 3