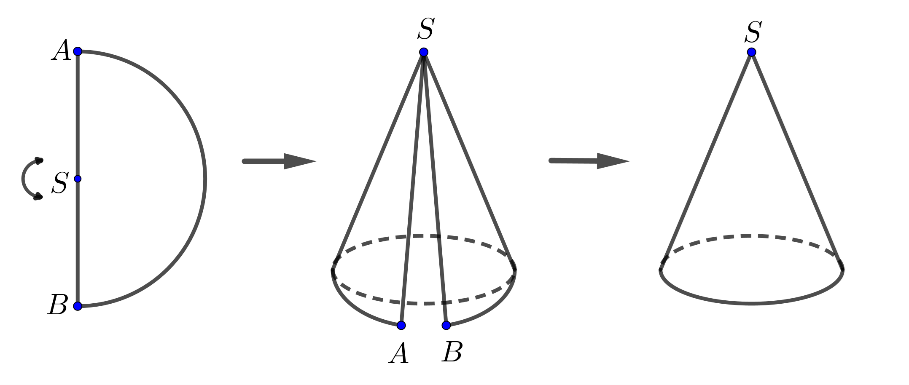
Cho một miếng tôn có dạng nửa hình tròn đường kính \(AB = 20\;cm\) và tâm là \(S\). Người ta làm một cái phễu có dạng hình nón không đáy bằng cách cuộn nửa hình tròn đó lại sao cho \(SA\) và \(SB\) sát vào nhau như hình vẽ. Tính thể tích của hình nón theo đơn vị \(c{m^3}\) (kết quả làm tròn đến hàng đơn vị, lấy \(\pi = 3,14\))

.

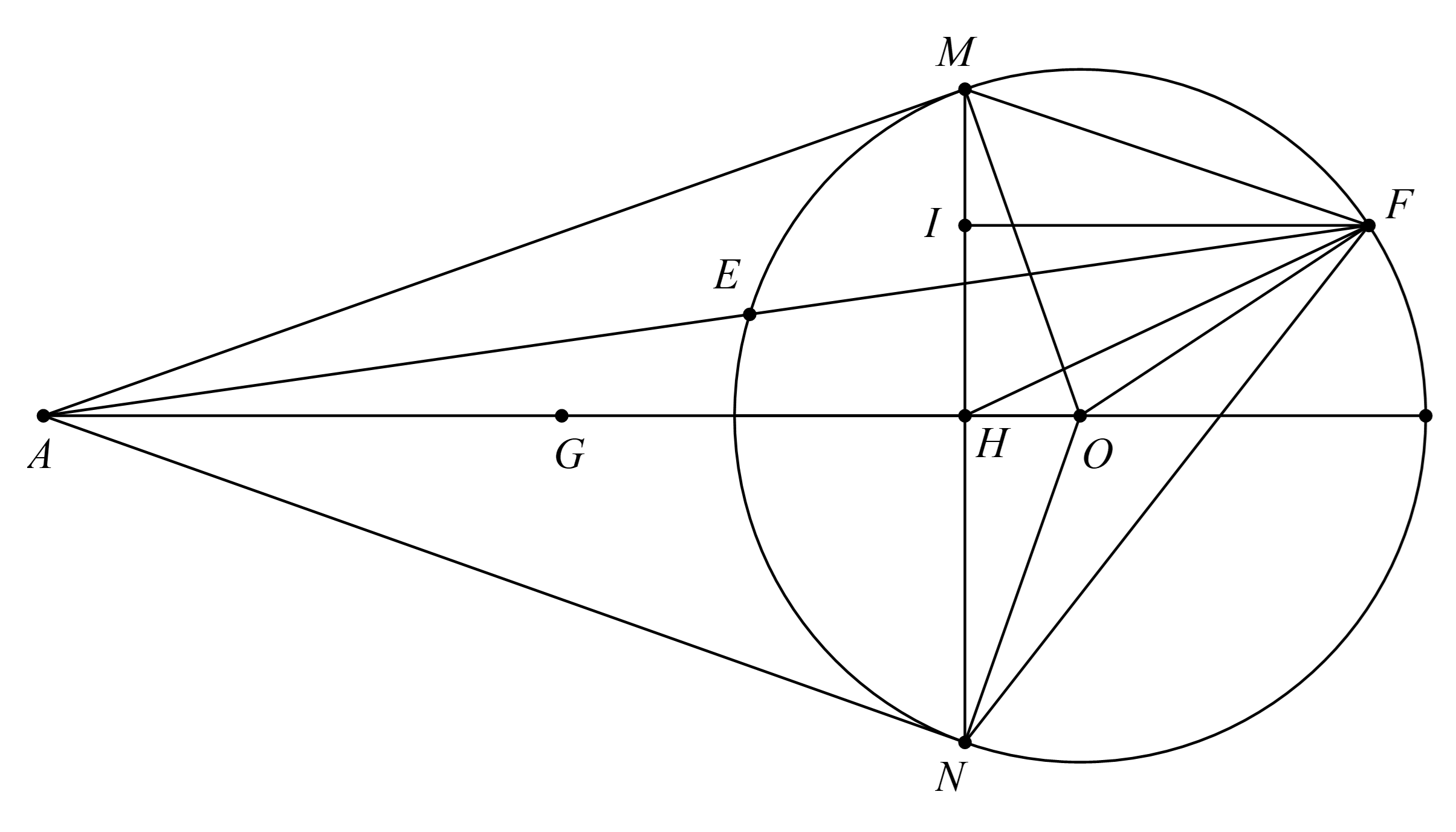
a) Chứng minh tứ giác \(AMON\)là tứ giác nội tiếp.

Gọi \(G\) là trung điểm của \(AO.\)

Xét \(\left( O \right)\) có \(AM\) là tiếp tuyến tại \(M\) (GT) nên \(AM \bot OM\) tại \(M \Rightarrow \widehat {AMO} = 90^\circ \)

Suy ra \(\Delta AMO\) nội tiếp đường tròn tâm \(G\) đường kính \(AO\)

Suy ra \(A,M,O \in \left( {G;\frac{{AO}}{2}} \right)\,\,\left( 1 \right)\)

Xét \((O)\) có \(AN\) là tiếp tuyến tại \(N\) (GT) nên \(AN \bot ON\) tại \(N \Rightarrow \widehat {ANO} = 90^\circ \)

Suy ra  \(\Delta ANO\) nội tiếp đường tròn tâm \(G\) đường kính \(AO\)

Suy ra \(A,N,O \in \left( {G;\frac{{AO}}{2}} \right)\,\,\left( 2 \right)\)

Từ \((1)\) và \((2)\) suy ra \(A,M,N,O \in \left( {G;\frac{{AO}}{2}} \right)\)

Do đó tứ giác\(AMNO\) là tứ giác nội tiếp đường tròn tâm \(G\) đường kính \(AO\).

Vậy tứ giác\(AMNO\) là tứ giác nội tiếp đường tròn tâm \(G\) đường kính \(AO\).

b) Xét tam giác \(AMO\) vuông tại \(M\) có \(AM = \sqrt {O{A^2} - O{M^2}}  = \sqrt {{{\left( {3R} \right)}^2} - {R^2}}  = 2\sqrt 2 R.\)

Theo giả thiết \(AM,\,AN\) là tiếp tuyến của đường tròn \(\left( {O;\,R} \right)\) nên \(AO\) là đường trung trực của \(MN\). Do đó \(AO \bot MN\) tại \(H\).

 Vậy \[AH = \frac{8}{3}R.\]

c) Ta có \(OH = AO - AH = 3R - \frac{{8R}}{3} = \frac{R}{3}.\)

Xét tam giác \(AMH\) vuông tại \(H\) có \(MH = \sqrt {A{M^2} - A{H^2}}  = \sqrt {{{\left( {2\sqrt 2 R} \right)}^2} - {{\left( {\frac{{8R}}{3}} \right)}^2}}  = \frac{{2\sqrt 2 R}}{3}.\)  

Từ đó \(MN = 2MH = \frac{{4\sqrt 2 R}}{3}.\)

Ta có \({S_{\Delta AMN}} = \frac{1}{2}AH.MN = \frac{1}{2}.\frac{{8R}}{3}.\frac{{4\sqrt 2 R}}{3} = \frac{{16\sqrt 2 {R^2}}}{9}.\)

Hạ \(FI \bot MN\) tại \(I.\)ta có:

\({S_{AMFN}} = {S_{\Delta AMN}} + {S_{\Delta FMN}} = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{1}{2}.MN.FI = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{1}{2}.\frac{{4\sqrt 2 R}}{3}.FI\)

\( = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{{2\sqrt 2 R}}{3}.FI\)

Do đó \({S_{AMFN}}\) lớn nhất khi\(FI\) lớn nhất.

Trong tam giác\(FIH\) vuông tại\(I\), ta có:  \(FI \le FH\)

mà \(FH \le OF + OH = R + \frac{R}{3} = \frac{{4R}}{3}\) nên \(FI \le \frac{{4R}}{3}.\)

Từ đó \(FI\) lớn nhất bằng \(\frac{{4R}}{3}\) khi \(d\) đi qua tâm \(O\).

Vậy \({S_{AMFN}}\) đạt giá trị lớn nhất bằng \({S_{AMFN}} = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{{2\sqrt 2 R}}{3}.\frac{{4R}}{3} = \frac{{8\sqrt 2 {R^2}}}{3}\) khi \(d\) đi qua tâm \(O\).

+ Không gian mẫu có 10 phần tử, cụ thể: (An; Bình), (An; Công), (Bình; Công), (Nguyệt; Yến), (An; Nguyệt), (An; Yến), (Bình; Nguyệt), (Bình; Yến), (Công; Nguyệt), (Công; Yến).

\(n\left( \Omega  \right) = 10.\)

Có 7 kết quả thuận lợi cho biến cố \(E\), cụ thể: (Nguyệt; Yến), (An; Nguyệt), (An; Yến), (Bình; Nguyệt), (Bình; Yến), (Công; Nguyệt), (Công; Yến).

\(n\left( E \right) = 10.\)

Vậy xác suất của biến cố \(E\) là \(P\left( E \right) = \frac{7}{{10}}\) .