Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi H là chận đường cao hạ từ đỉnh A của tam giác ABC. Chứng minh \[\widehat {BAH} = \widehat {OAC}\].
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi H là chận đường cao hạ từ đỉnh A của tam giác ABC. Chứng minh \[\widehat {BAH} = \widehat {OAC}\].
Quảng cáo
Trả lời:
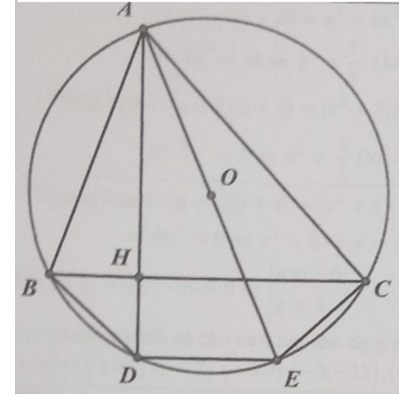
Kẻ đường kính AE của đường tròn (O). Ta thấy \[\widehat {ACE} = {90^o}\](Góc nội tiếp chắn nửa đường tròn)
Từ đó \[\widehat {OAC}{\rm{ }} + {\rm{ }}\widehat {AEC}{\rm{ }} = {\rm{ }}90^\circ \] (1)
Theo gt \[\widehat {BAH}{\rm{ }} + {\rm{ }}\widehat {ABC}{\rm{ }} = {\rm{ }}90^\circ \] (2)
Hơn nữa \[\widehat {AEC}{\rm{ }} = {\rm{ }}\widehat {ABC}{\rm{ }}\](Cùng chắn cung AC) (3)
Từ (1), (2) và (3) suy ra \[\widehat {BAH} = \widehat {OAC}\]Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
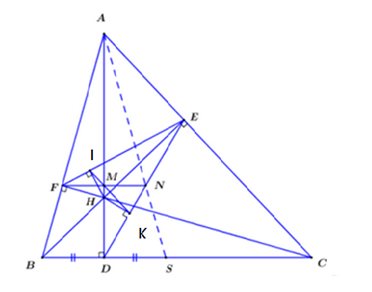
Do BE là phân giác trong góc FED nên HK = HI
\[ \Rightarrow \widehat {HKM} = \widehat {HIM\;\;}\;\;\;\;(1)\]
Ta có \[\widehat {MHF} = 90^\circ - \widehat {FAH} = 90^\circ - \widehat {FEH} = 90^\circ - \widehat {IEH}\]
Và \[\widehat {KIE} = 90^\circ - \widehat {IEH} \Rightarrow \widehat {MHF} = \widehat {KIE}\]
Do đó tứ giác FIMH nội tiếp \[ \Rightarrow \widehat {HIM} = \widehat {HFM}\] (2)Do tứ giác FIMH nội tiếp
\[ \Rightarrow \widehat {FMH} = \widehat {HIF} = 90^\circ \Rightarrow \widehat {HMN} = 90^\circ \]
và \[\widehat {HKN} = 90^\circ \]nên tứ giác HMNK nội tiếp
\[ \Rightarrow \widehat {HNM} = \widehat {HKM}\] (3)Từ (1), (2) và (3) suy ra \[\widehat {HNM} = \widehat {HFM}\]nên FHN cân tại H có đường cao MH
\[ \Rightarrow \]MF = MN \[ \Rightarrow \]FAN cân tại A
Từ đó ta chứng minh được A, N, S thẳng hàng.Lời giải
Biến đổi pt ở đầu bài ta được(y+1)(y+2) = x4 + x2 + 20
Ta thấy x4 + x2 < x4 + x2 + 20 \[ \le \] x4 + x2 + 20 + 8 x2
\[ \Leftrightarrow {x^2}\left( {{x^2} + 1} \right) < \left( {y + 1} \right)\left( {y + 2} \right) \le \left( {{x^2} + 4} \right)\left( {{x^2} + 5} \right)\]
Vì x, y là các số nguyên nên ta xét các TH sau:
TH1:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 1} \right)\left( {{x^2} + 2} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 3{x^2} + 2\\ \Leftrightarrow 2{x^2} = 18 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\end{array}\]
Thế vào pt đã cho ta có \[{y^2} + 3y - 108 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 9\\y = - 12\end{array} \right.(t/m)\]
TH2:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 2} \right)\left( {{x^2} + 3} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 5{x^2} + 6\\ \Leftrightarrow 4{x^2} = 14 \Leftrightarrow {x^2} = \frac{7}{2}(loai)\end{array}\]
TH3:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 3} \right)\left( {{x^2} + 4} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 7{x^2} + 12\\ \Leftrightarrow 6{x^2} = 8 \Leftrightarrow {x^2} = \frac{4}{3}(loai)\end{array}\]
TH4:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 4} \right)\left( {{x^2} + 5} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 9{x^2} + 20\\ \Leftrightarrow 8{x^2} = 0 \Leftrightarrow x = 0(t/m)\end{array}\]
Khi đó \[{y^2} + 3y - 18 = 0 \Leftrightarrow \left[ \begin{array}{l}y = - 6\\y = 3\end{array} \right.(t/m)\]
Vậy pt đã cho có 6 nghiệm nguyên
(x;y) = (3;9), (3, -12), (-3, 9), (-3;-12); (0, -6), (0;3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.