Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 sở GD&ĐT Ninh Thuận có đáp án
69 người thi tuần này 4.6 69 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
Lời giải
Gọi vận tốc của thuyền khi nước yên lặng là x (km/h)
Gọi vận tốc của dòng nước là y (km/h) (x, y >0)
Thời gian xuôi dòng là \[\frac{{80}}{{x + y}}(h)\]
Thời gian ngược dòng là \[\frac{{80}}{{x - y}}(h)\]
Chiếc thuyền xuôi dòng và ngược dòng trên khúc sông dài 80 km hết 9h nên ta có pt: \[\frac{{80}}{{x + y}} + \frac{{80}}{{x - y}} = 9\]
Thời gian chiếc thuyền ngược dòng trên khúc sông này nhiều hơn xuôi dòng 1 giờ nên ta có pt: \[\frac{{80}}{{x - y}} = \frac{{80}}{{x + y}} + 1\]
Từ đó ta có hpt: \[\left\{ \begin{array}{l}\frac{{80}}{{x - y}} = \frac{{80}}{{x + y}} + 1\\\frac{{80}}{{x + y}} + \frac{{80}}{{x - y}} = 9\end{array} \right.\]
\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{{x + y}} = \frac{1}{{20}}\\\frac{1}{{x - y}} = \frac{1}{{16}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + y = 20\\x - y = 16\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 18\\y = 2\end{array} \right.\end{array}\]
Vậy vận tốc của dòng nước là 2 km/h
Lời giải
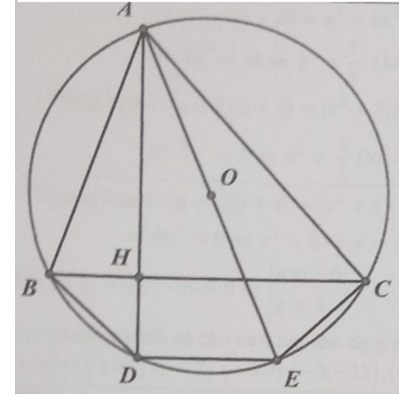
Kẻ đường kính AE của đường tròn (O). Ta thấy \[\widehat {ACE} = {90^o}\](Góc nội tiếp chắn nửa đường tròn)
Từ đó \[\widehat {OAC}{\rm{ }} + {\rm{ }}\widehat {AEC}{\rm{ }} = {\rm{ }}90^\circ \] (1)
Theo gt \[\widehat {BAH}{\rm{ }} + {\rm{ }}\widehat {ABC}{\rm{ }} = {\rm{ }}90^\circ \] (2)
Hơn nữa \[\widehat {AEC}{\rm{ }} = {\rm{ }}\widehat {ABC}{\rm{ }}\](Cùng chắn cung AC) (3)
Từ (1), (2) và (3) suy ra \[\widehat {BAH} = \widehat {OAC}\]Lời giải
Biến đổi pt ở đầu bài ta được(y+1)(y+2) = x4 + x2 + 20
Ta thấy x4 + x2 < x4 + x2 + 20 \[ \le \] x4 + x2 + 20 + 8 x2
\[ \Leftrightarrow {x^2}\left( {{x^2} + 1} \right) < \left( {y + 1} \right)\left( {y + 2} \right) \le \left( {{x^2} + 4} \right)\left( {{x^2} + 5} \right)\]
Vì x, y là các số nguyên nên ta xét các TH sau:
TH1:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 1} \right)\left( {{x^2} + 2} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 3{x^2} + 2\\ \Leftrightarrow 2{x^2} = 18 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\end{array}\]
Thế vào pt đã cho ta có \[{y^2} + 3y - 108 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 9\\y = - 12\end{array} \right.(t/m)\]
TH2:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 2} \right)\left( {{x^2} + 3} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 5{x^2} + 6\\ \Leftrightarrow 4{x^2} = 14 \Leftrightarrow {x^2} = \frac{7}{2}(loai)\end{array}\]
TH3:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 3} \right)\left( {{x^2} + 4} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 7{x^2} + 12\\ \Leftrightarrow 6{x^2} = 8 \Leftrightarrow {x^2} = \frac{4}{3}(loai)\end{array}\]
TH4:
\[\begin{array}{l}\left( {y + 1} \right)\left( {y + 2} \right) = \left( {{x^2} + 4} \right)\left( {{x^2} + 5} \right)\\ \Leftrightarrow {x^4} + {x^2} + 20 = {x^4} + 9{x^2} + 20\\ \Leftrightarrow 8{x^2} = 0 \Leftrightarrow x = 0(t/m)\end{array}\]
Khi đó \[{y^2} + 3y - 18 = 0 \Leftrightarrow \left[ \begin{array}{l}y = - 6\\y = 3\end{array} \right.(t/m)\]
Vậy pt đã cho có 6 nghiệm nguyên
(x;y) = (3;9), (3, -12), (-3, 9), (-3;-12); (0, -6), (0;3)
Lời giải
Đặt p = x+y+z; q = xy + yz + zx
Điều cần cm trở thành \[\frac{1}{q} - \frac{1}{p} \le \frac{2}{3} \Leftrightarrow q \ge \frac{{3p}}{{2p + 3}}\]
Mà \[{\left( {xy + yz + zx} \right)^2} \ge 3xyz\left( {x + y + z} \right) = \frac{3}{8}\left( {x + y + z} \right) \Leftrightarrow {q^2} \ge \frac{3}{8}p\]
Nên ta chỉ cần cm \[\frac{3}{8}p \ge {\left( {\frac{{3p}}{{2p + 3}}} \right)^2}\]
Thật vậy \[\frac{3}{8}p \ge {\left( {\frac{{3p}}{{2p + 3}}} \right)^2} \Leftrightarrow 4{p^2} - 12p + 9 \ge 0\]
\[ \Leftrightarrow {\left( {2p - 3} \right)^2} \ge 0\] (Luôn đúng). Suy ra đpcm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.