Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?

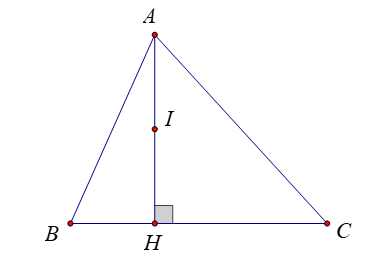
Gọi \(AH\) là đường cao của tam giác \(ABC\).

Ta có \(AH \bot BC\).

Ta có \(\overrightarrow {{n_{BC}}} = \left( {1;1} \right)\) là một vectơ pháp tuyến của đường thẳng \(BC\).

Suy ra \(\overrightarrow {{u_{BC}}} = \left( { - 1;1} \right)\) là một vectơ chỉ phương của \(BC\).

Lại có \(AH \bot BC\) nên \(AH\) nhận \(\overrightarrow {{u_{BC}}} = \left( { - 1;1} \right)\) làm vectơ pháp tuyến.

Khi đó đường thẳng \(AH\) có phương trình là \( - \left( {x + 1} \right) + \left( {y + 2} \right) = 0 \Leftrightarrow - x + y + 1 = 0\).

Tọa độ điểm \(H\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y + 4 = 0\\ - x + y + 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{3}{2}\\y = - \frac{5}{2}\end{array} \right.\)\( \Rightarrow H\left( {\frac{{ - 3}}{2};\frac{{ - 5}}{2}} \right)\).

Gọi \(I\) là trung điểm của \(AH\) nên \(I\left( { - \frac{5}{4}; - \frac{9}{4}} \right)\).

Đường trung bình D ứng với cạnh đáy \(BC\) có dạng \(x + y + c = 0\).

Lại có \(\Delta \) đi qua \(I\) nên \( - \frac{5}{4} - \frac{9}{4} + c = 0 \Rightarrow c = \frac{7}{2}\).

Vậy \(\Delta :x + y + \frac{7}{2} = 0\) hay \(\Delta :2x + 2y + 7 = 0\)

Vì \(d//\Delta \) nên \(d:2x - y + c = 0,c \ne 1\).

Vì \(d\) đi qua điểm \(M\left( {1; - 2} \right)\) nên \(2 \cdot 1 - \left( { - 2} \right) + c = 0 \Rightarrow c = - 4\).

Vậy \(d:2x - y - 4 = 0\). Suy ra \(b = - 1;c = - 4\).

Vậy \(T = 2b + c = - 6\).