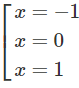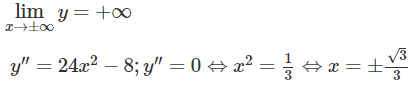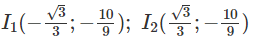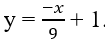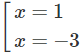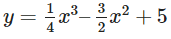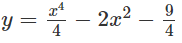Câu hỏi:
12/07/2024 4,545Cho hàm số y = 2 − 4 (1)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
b) Với giá trị nào của m, phương trình | − 2| = m có đúng 6 nghiệm thực phân biệt?
(Đề thi đại học năm 2009; khối B)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tập xác định: D = R
y′=0 ⇔ 
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; +)
Hàm số nghịch biến trên mỗi khoảng (−; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; = −2
Đồ thị có hai điểm uốn:
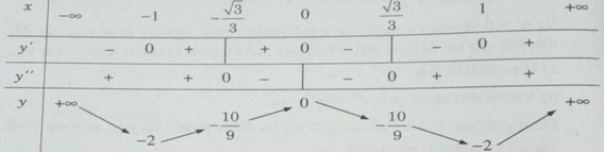
Bảng biến thiên:
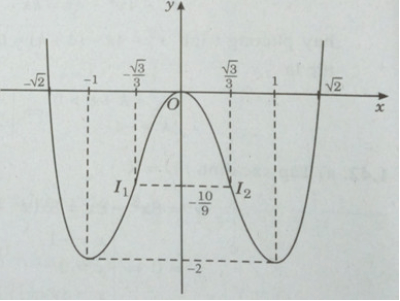
Đồ thị:
Đồ thị cắt trục hoành tại:
b) Ta có: | − 2| = m
⇔ 2 | − 2| = 2m
⇔|2( − 2)| = 2m
⇔|2 − 4| = 2m
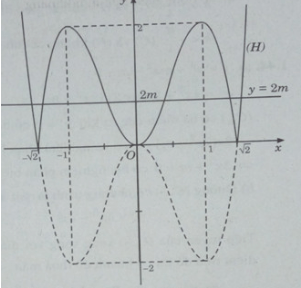
Từ đồ thị hàm số y = 2 – 4 có thể suy ra đồ thị của hàm số y = |2 − 4| như sau:
Phương trình: |2 − 4| = 2m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m có 6 nghiệm phân biệt với đồ thị (H)
⇔ 0 < 2m < 2
⇔ 0 < m < 1
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: C.
y' = 4 - 4x = 4x( - 1). Ta có
y - y(-2) = y'(-2)(x + 2) ⇔ y - 8 = -24(x + 2) ⇔ y = -24x - 40.
Lời giải
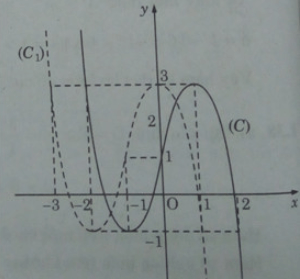
a)
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − + 3(x + 1) + 1 hay f(x) = − + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = − 3x – 4
c) Ta có: = 3x + m (1)
⇔ − 3x – 4 = m – 4
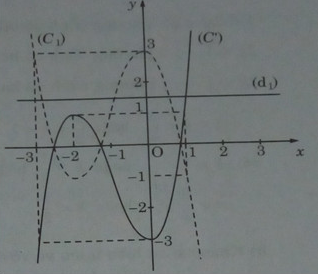
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 – 3
g′(x) = 9 ⇔ 
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)