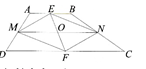
Cho hình thang ABCD (AB // CD). Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi O là trung điểm của EF. Qua O vẽ đường thẳng song song với AB, cắt AD và BC theo thứ tự tại M và N.
          a) Tứ giác EMFN là hình gì ?
          b) Hình thang ABCD có thêm điều kiện gì để EMFN là hình thoi.
          c) Hình thang ABCD có thêm điều kiện gì để EMFN là hình vuông

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) ABCD là hình thang nên AE//DF Þ AEFD là hình thang. O là trung điểm EF, OM/AE Þ M là trung điểm AD (tính chất đường trung bình của hình thang)

Þ ME//FN//BD và ME = FN = 0.5.AC Þ AC = BD

Þ ABCD là hình thang cân.

c) Nếu EMFN là hình vuông thì ME ^ EN Þ BD ^ AC nên ABCD là hình thang cân có hai đường chéo vuông góc.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

a) DDAE = DBAF (c.g.c)

$\Rightarrow \hat{D A E} = \hat{B A F}$ và AE = AF

Mà $\hat{E A D} + \hat{E A B} = 90^{0} = > \hat{E A B} + \hat{B A F} = 90^{0}$

Þ DAEF vuông cân tại A.

b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);

Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.

c) Do K đối xứng với A qua I nên I là trung điểm của AK.

Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.

Vậy AFKE là hình vuông.

Câu 2

Xem đáp án

Lời giải

a) Vì ABDE, ACFG là các hình vuông nên ta có E, A, C thẳng hàng và B, A, G cũng thẳng hàng (1) và EC = BG.

Mà $\hat{E B A} = \hat{A G C}$ = 45⁰ (2).

Từ (1) và (2)

Suy ra EB//CG & EC = BG Þ EBCG là hình thang cân.

b) Chứng minh AEKG là hình chữ nhật, mà M là trung điểm EG nên K, A, M thẳng hàng.

c) Gọi H = MA Ç BC

Vì BEGC là hình thang cân nên DBEG = DEBC (c-g-c) Þ $\hat{E C B} = \hat{E G B}$ mà $\hat{E G A} = \hat{M A G} = \hat{B A H}$

Þ $\hat{B A H} + \hat{A B C} = \hat{E C B} + \hat{A B C}$ = 90⁰ Þ MA ^BC tại H.

d) DABK = DBDC vì AB = DB, KA = EG = BC, $\hat{B A K} = \hat{D B C} \Rightarrow \hat{B K A} = \hat{B C D}$ mà KA ^ BC Þ CD ^ BK.

Chứng minh tương tự ta cũng có BF ^ KC.

Þ DKBC cosBF, CD, AM là 3 đường cao Þ đồng quy tại trực tâm I

Câu 3