Câu hỏi:
12/07/2024 995
Quan sát đồ thị hàm số bậc hai y = ax2 + bx + c ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Tọa độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà y ≤ 0.
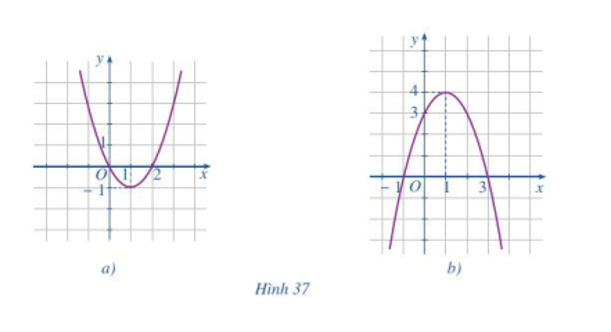
Quan sát đồ thị hàm số bậc hai y = ax2 + bx + c ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Tọa độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà y ≤ 0.
Câu hỏi trong đề:
Bài tập cuối chương III có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
* Hình 37a: Quan sát đồ thị ta thấy:
a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu “+”.
b) Tọa độ đỉnh I(1; – 1), trục đối xứng x = 1.
c) Do hệ số a > 0 nên hàm số đồng biến trên khoảng (1; + ∞).
d) Hàm số nghịch biến trên khoảng (– ∞; 1).
e) Phần parabol nằm phía trên trục hoành tương ứng với các khoảng (– ∞; 0) và (2; + ∞) nên hàm số y > 0 trên các khoảng giá trị của x là (– ∞; 0) ∪ (2; + ∞).
g) Phần parabol phía dưới trục hoành tương ứng với khoảng (0; 2) nên hàm số y < 0 trên (0; 2). Vậy khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2].
* Hình 37b: Quan sát đồ thị ta thấy,
a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu “–”.
b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1.
c) Do hệ số a < 0 nên hàm số đồng biến trên khoảng (– ∞; 1).
d) Hàm số nghịch biến trên khoảng (1; +∞).
e) Phần parabol nằm phía trên trục hoành tương ứng với khoảng (– 1; 3) nên khoảng giá trị của x là (– 1; 3) thì y > 0.
g) Phần parabol nằm phía dưới trục hoành tương ứng với các khoảng (– ∞; – 1) và (3; + ∞) nên khoảng giá trị của x để y ≤ 0 là (– ∞; – 1] ∪ [3; + ∞).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Xem đáp án »
12/07/2024
16,154
Câu 2:
Giải các bất phương trình sau:
a) 2x2 + 3x + 1 ≥ 0;
b) – 3x2 + x + 1 > 0;
c) 4x2 + 4x + 1 ≥ 0;
d) – 16x2 + 8x – 1 < 0;
e) 2x2 + x + 3 < 0;
g) – 3x2 + 4x – 5 < 0.
Giải các bất phương trình sau:
a) 2x2 + 3x + 1 ≥ 0;
b) – 3x2 + x + 1 > 0;
c) 4x2 + 4x + 1 ≥ 0;
d) – 16x2 + 8x – 1 < 0;
e) 2x2 + x + 3 < 0;
g) – 3x2 + 4x – 5 < 0.
Xem đáp án »
12/07/2024
8,121
Câu 3:
Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:
Gói A: Giá cước 190 000 đồng/tháng.
Nếu trả tiền cước ngay 6 tháng thì sẽ được tặng thêm 1 tháng.
Nếu trả tiền cước ngay 12 tháng thì sẽ được tặng thêm 2 tháng.
Gói B: Giá cước 189 000 đồng/tháng.
Nếu trả tiền cước ngay 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng.
Nếu trả tiền cước ngay 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng.
Giả sử số tháng sử dụng Internet là x (x nguyên dương).
a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian dùng không quá 15 tháng.
b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào?
Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:
Gói A: Giá cước 190 000 đồng/tháng.
Nếu trả tiền cước ngay 6 tháng thì sẽ được tặng thêm 1 tháng.
Nếu trả tiền cước ngay 12 tháng thì sẽ được tặng thêm 2 tháng.
Gói B: Giá cước 189 000 đồng/tháng.
Nếu trả tiền cước ngay 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng.
Nếu trả tiền cước ngay 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng.
Giả sử số tháng sử dụng Internet là x (x nguyên dương).
a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian dùng không quá 15 tháng.
b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào?
Xem đáp án »
12/07/2024
6,195
Câu 4:
Vẽ đồ thị của mỗi hàm số sau:
a) y = x2 – 3x – 4;
b) y = x2 + 2x + 1;
c) y = – x2 + 2x – 2.
Vẽ đồ thị của mỗi hàm số sau:
a) y = x2 – 3x – 4;
b) y = x2 + 2x + 1;
c) y = – x2 + 2x – 2.
Xem đáp án »
12/07/2024
5,985
Câu 5:
Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a) f(x) = – 3x2 + 4x – 1;
b) f(x) = x2 – x – 12;
c) f(x) = 16x2 + 24x + 9.
Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a) f(x) = – 3x2 + 4x – 1;
b) f(x) = x2 – x – 12;
c) f(x) = 16x2 + 24x + 9.
Xem đáp án »
12/07/2024
1,142
về câu hỏi!