Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
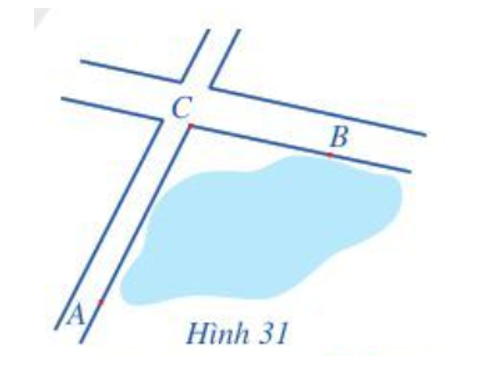
Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Câu hỏi trong đề: Bài tập Giải tam giác có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nối A với B, ba vị trí A, B, C tạo thành 3 đỉnh của tam giác ABC.
Đổi 1 km = 1 000 m.
Tam giác ABC có AC = 1 000 m, CB = 800 m, .
Áp dụng định lí côsin ta có:
AB2 = AC2 + CB2 – 2 . AC . CB . cosACB
= 1 0002 + 8002 – 2 . 1 000 . 800 . cos 105°
≈ 2 054 110,5
Do đó: AB ≈ 1 433,2 m.
Vậy khoảng cách AB khoảng 1 433,2 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Giả sử C là vị trí của ngọn hải đăng, kẻ CH vuông góc AB thì CH là khoảng cách giữa ngọn hải đăng và bờ.
Ta có: là góc ngoài tại đỉnh B của tam giác ABC.
Nên .
.
Áp dụng định lí sin trong tam giác ABC ta có:
.
Tam giác CBH vuông tại H nên
.
Vậy ngọn hải đăng cách bờ biển khoảng 41 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Cách 1: áp dụng định lí sin và côsin
Áp dụng định lí sin trong tam giác ABC ta có:
.
Do đó: .
Lại có (định lí tổng ba góc trong tam giác)
.
Áp dụng định lí côsin trong tam giác ABC ta có:
AC2 = AB2 + BC2 – 2 . AB . AC . sin B = 52 + 72 – 2 . 5 . 7 . cos 22° ≈ 9
⇒ AC ≈ 3.
Cách 2: Dựng thêm đường cao và sử dụng định lí Pythagore.
Dựng đường cao CH của tam giác ABC.
Đặt AH = x.
Ta có: ( kề bù).
.
Tam giác ACH vuông tại H nên
.
Áp dụng định lí Pythagore ta tính được: .
Và BC2 = BH2 + CH2 = (BA + AH)2 + CH2
Thay số: 72 = (5 + x)2 + 3x2 (1)
Giải phương trình (1) ta được x = 1,5 là giá trị thỏa mãn.
Suy ra AC = 2x = 2 . 1,5 = 3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập