Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;1), B(0;1;2), C(-2;1;4) và mặt phẳng (P): x-y+z+2=0. Tìm điểm N(P) sao cho đạt giá trị nhỏ nhất.
A. N(-2;0;1)
B.
C.
D. N(-1;2;1)
Quảng cáo
Trả lời:
Đáp án D
Phương pháp giải: Xét đẳng thức vectơ, đưa về hình chiếu của điểm trên mặt phẳng
Lời giải:
Gọi M(a;b;c) thỏa mãn đẳng thức vectơ
![]()
=2(1-a;1-b;1-c)+(0-a; 1-b;2-c)+(-2-1;1-b;4-c)=0
![]()
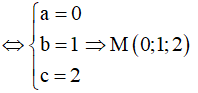
Khi đó
![]()
![]()
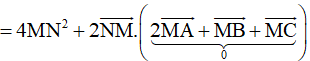
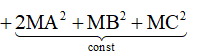
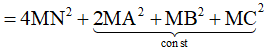
![]()
<=> N là hình chiếu của M trên (P) =>MN(P)
Phương trình đường thẳng MN là
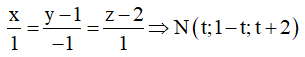
![]()
![]()
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. (1;0;3)
B. (-1;1;-1)
C. (2;-2;3)
D. (1;1;-1)
Lời giải
Đáp án B
Phương pháp giải: Viết phương trình đường thẳng vuông góc với mặt và đi qua điểm, tọa độ giao điểm của đường thẳng và mặt phẳng chính là tọa độ hình chiếu của điểm
Lời giải:
Gọi H là hình chiếu của A trên
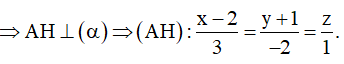
![]()
![]()
![]()
=> t= - 1
Vậy tọa độ điểm cần tìm là H(-1;1;-1)
Lời giải
Đáp án A
Phương pháp:
+) Viết phương trình mặt phẳng (ABC) ở dạng đoạn chắn, thay tọa độ điểm M vào pt mặt phẳng (ABC).
+) (ABC) tiếp xúc với mặt cầu (S) tâm I bán kính R <=> d(I;(ABC))=R
Cách giải:
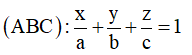
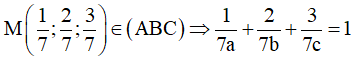
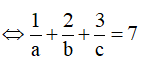
(ABC) tiếp xúc với mặt cầu (S) có tâm I và bán kính
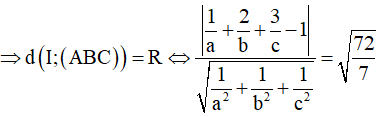
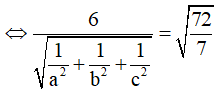
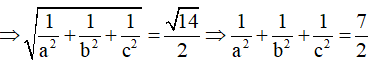
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. H(3;0;2)
B. H(-1;4;4)
C. H(2;0;3)
D. H(4;4;-1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. -2 - x
B. 3x + 2
C. 3x - 2
D. x + 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Cho mặt phẳng đi qua M(1;-3;4) và song song với mặt phẳng : 6x +2y-z-7=0. Phương trình mặt phẳng là:
A. 6x +2y-z+8=0.
B. 6x +2y-z+4=0.
C. 6x +2y-z-4=0.
D. 6x +2y-z-17=0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.