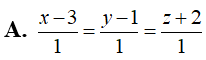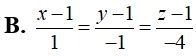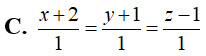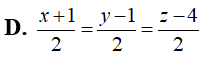Trong không gian Oxyz, cho mặt cầu
và M(4;5;3). Qua M kẻ các tia Mx, My, Mz đôi một vuông góc với nhau và cắt mặt cầu tại các điểm thứ hai tương ứng là A, B, C. Biết mặt phẳng (ABC) luôn đi qua một điểm cố định H(a;b;c). Tính a+3b-c.
A. 9.
B. 14.
C. 11.
D. 20.
Quảng cáo
Trả lời:
Chọn A
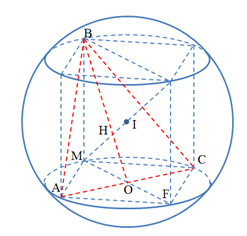
Ta có M(4;6;3) nằm trên mặt cầu (S) tâm I(1;2;3) bán kính R =5.
Dựng hình hộp chữ nhật nội tiếp hình cầu, có ba cạnh làMA, MB, MC
Ta có tâm I(1;2;3) của mặt cầu cũng là tâm của hình hộp chữ nhật
Gọi O là tâm đường tròn ngoại tiếp tứ giác MAFC
Trong mặt phẳng (MBF)
![]()
![]()
Do H là trọng tâm của tam giác MBF nên MH=MI
Do I, M cố định nên H cố định (2)
Từ (1) và (2) Suy ra (ABC) luôn đi qua điểm cố định H.
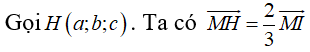
![]()
![]()
Ta được
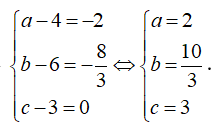
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn B
Cách 1:
![]()
Gọi M,N lần lượt là trung điểm AB, BC
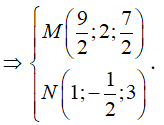
Gọi là véc tơ pháp tuyến của mặt phẳng (ABC).
![]()
![]()
I là tâm đường tròn ngoại tiếp tam giác ABC
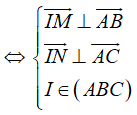
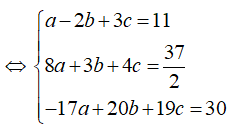
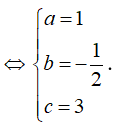
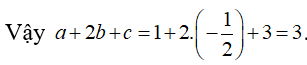
Cách 2:
Ta có
![]()
![]()
=> Tam giác ABC vuông tại B
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên I là trung điểm của AC.
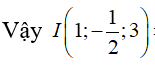
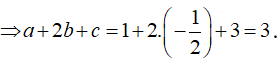
Lời giải
Chọn B
Do G là trọng tâm tam giác ABC => G(2;3;1).
Gọi H là hình chiếu vuông góc của G trên mặt phẳng (Oxz), khi đó GH là khoảng cách từ G đến mặt phẳng (Oxz), ta có:
![]()
Với M là điểm thay đổi trên mặt phẳng (Oxz)
![]()
do đó GM ngắn nhất
Vậy độ dài GM ngắn nhất bằng 3
Câu 3
A. T = - 3
B. T = 1
C. T = 3
D. T = - 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.