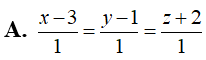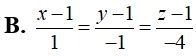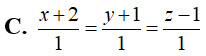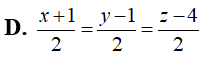Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa đường thẳng d: x-11=y+2-1=z-2 và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt phẳng (P) A. E(-3;0;4) B. M(3;0;...

Câu hỏi:

10/01/2020 2,031

Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa đường thẳng $d : \frac{x - 1}{1} = \frac{y + 2}{- 1} = \frac{z}{- 2}$ và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt phẳng (P)

A. E(-3;0;4)

B. M(3;0;2)

C. N(-1;-2;-1)

D. F(1;2;1)

Xem lời giải

Câu hỏi trong đề: Bài tập Hình học không gian từ đề thi đại học có lời giải chi tiết !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Cách 1:

Đường thẳng d qua điểm M(1;-2;0), có véc tơ chỉ phương $\vec{a} = (1; - 1; - 2)$ và trục Oy có véc tơ chỉ phương $\vec{j} = (0; 1; 0)$ .

là một véc tơ pháp tuyến của mặt phẳng (P).

Gọi $φ$ là góc giữa mặt phẳng (P) và trục Oy $(0 \leq φ \leq \frac{π}{2})$

Ta có

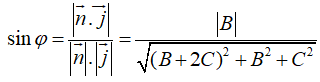
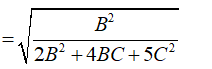
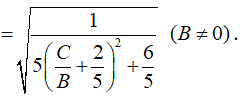
Vì hàm số sin $φ$ tăng liên tục trên $(0; \frac{π}{2})$ nên $φ$ đạt giá trị lớn nhất khi sin $φ$ lớn nhất

Lúc đó

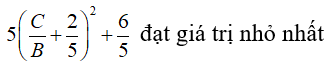
Chọn B= 5; C=-2, A = 1 => $\vec{n} = (1; 5; - 2)$

Phương trình mặt phẳng (P) qua điểm M, có véc tơ pháp tuyến $\vec{n} = (1; 5; - 2)$ là:

Thế tọa độ N(-1;-2;-1) vào phương trình mặt phẳng (P): -1+5(-2)-2(-1)+9=0 (luôn đúng).

Vậy điểm N(-1;-2;-1) thuộc mặt phẳng (P).

Cách 2:

Xét bài toán tổng quát: Cho hai đường thẳng $∆_{1}, ∆_{2}$ phân biệt và không song song với nhau. Viết phương trình mặt phẳng (P) chứa đường thẳng $∆_{1}$ và tạo với $∆_{2}$ một góc lớn nhất.

Phương pháp giải:

+) Vẽ một đường thẳng $∆_{3}$ bất kỳ song song với $∆_{2}$ và cắt $∆_{1}$ tại M. Gọi B là điểm cố định trên $∆_{3}$ và H là hình chiếu vuông góc của B lên mp (P), kẻ BA $⊥ ∆_{1}$

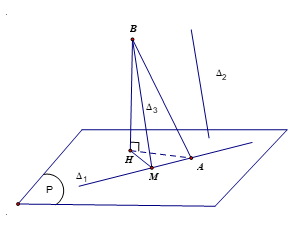
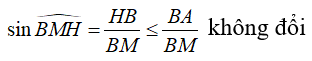
và (P) chứa $∆_{1}$ và vuông góc với mặt phẳng ( $∆_{1}$ , $∆_{2}$ )

Vậy (P) có VTPT là

Áp dụng:

Phương trình mặt phẳng (P) qua điểm M(1;-2;0), có véc tơ pháp tuyến là

Vậy điểm N(-1;-2;-1) thuộc mặt phẳng (P).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz cho các điểm A(5;1;5), B(4;3;2), C(-3;-2;1). Điểm I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a+2b+c?

A. 1

B. 3

C. 6

D. -9

Lời giải

Chọn B

Cách 1:

Gọi M,N lần lượt là trung điểm AB, BC

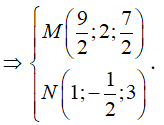
Gọi $\vec{n}$ là véc tơ pháp tuyến của mặt phẳng (ABC).

I là tâm đường tròn ngoại tiếp tam giác ABC

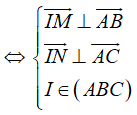
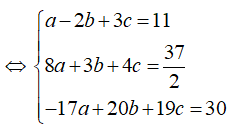
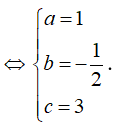
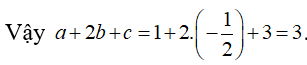
Cách 2:

Ta có

=> Tam giác ABC vuông tại B

Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên I là trung điểm của AC.

Câu 2

Trong không gian Oxyz, cho tam giác ABC với A(1;2;5), B(3;4;1), C(2;3;-3). Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên (Oxz). Độ dài GM ngắn nhất bằng

A. 2

B. 3

C. 4

D. 1

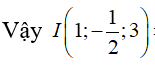
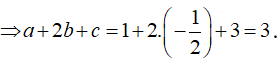
Lời giải

Chọn B

Do G là trọng tâm tam giác ABC => G(2;3;1).

Gọi H là hình chiếu vuông góc của G trên mặt phẳng (Oxz), khi đó GH là khoảng cách từ G đến mặt phẳng (Oxz), ta có:

Với M là điểm thay đổi trên mặt phẳng (Oxz)

do đó GM ngắn nhất $\Leftrightarrow M \equiv H$

Vậy độ dài GM ngắn nhất bằng 3

Câu 3

Trong không gian Oxyz, cho hình thang cân ABCD có các đáy lần lượt là AB, CD. Biết A(3;1;-2), B(-1;3;2), C(-6;3;6), và D(a;b;c) với a, b, c $\in ℝ$ . Tính T = a+ b+ c.

A. T = - 3

B. T = 1

C. T = 3

D. T = - 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ tọa Oxyz, cho vectơ $\vec{a} = (1; - 2; 4)$ , $\vec{b} = (x_{0}; y_{0}; z_{0})$ cùng phương với vectơ $\vec{a}$ . Biết vectơ $\vec{b}$ tạo với tia Oy một góc nhọn và $|\vec{b}| = \sqrt{21}$ . Giá trị của tổng $x_{0} + y_{0} + z_{0}$ bằng

A. -3

B. 6

C. -6

D. 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng

A. $\frac{\sqrt{3}}{2}$

B. $\frac{2 \sqrt{3}}{3}$

C. $\frac{\sqrt{5}}{5}$

D. $\frac{2 \sqrt{5}}{5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho 2 đường thẳng $d : \{\begin{cases} x = - 1 - 2 t \\ y = t \\ z = - 1 + 3 t \end{cases}$ , $d' : \{\begin{cases} x = 2 + t' \\ y = - 1 + 2 t' \\ z = - 2 t' \end{cases}$ và mặt phẳng (P): x + y + z + 2 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d và d' có phương trình là

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian Oxyz, cho mặt cầu

$(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 25$ và M(4;5;3). Qua M kẻ các tia Mx, My, Mz đôi một vuông góc với nhau và cắt mặt cầu tại các điểm thứ hai tương ứng là A, B, C. Biết mặt phẳng (ABC) luôn đi qua một điểm cố định H(a;b;c). Tính a+3b-c.

A. 9.

B. 14.

C. 11.

D. 20.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa đường thẳng d: x-11=y+2-1=z-2 và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt phẳng (P)

Bình luận

Trong không gian Oxyz cho các điểm A(5;1;5), B(4;3;2), C(-3;-2;1). Điểm I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a+2b+c?

Trong không gian Oxyz, cho tam giác ABC với A(1;2;5), B(3;4;1), C(2;3;-3). Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên (Oxz). Độ dài GM ngắn nhất bằng

Trong không gian Oxyz, cho hình thang cân ABCD có các đáy lần lượt là AB, CD. Biết A(3;1;-2), B(-1;3;2), C(-6;3;6), và D(a;b;c) với a, b, c ∈ℝ. Tính T = a+ b+ c.

Trong không gian với hệ tọa Oxyz, cho vectơ a→=(1;-2;4), b→=x0;y0;z0 cùng phương với vectơ a→. Biết vectơ b→ tạo với tia Oy một góc nhọn và b→=21. Giá trị của tổng x0+y0+z0 bằng

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng

Trong không gian Oxyz, cho 2 đường thẳng d: x=-1-2ty=tz=-1+3t , d': x=2+t'y=-1+2t'z=-2t' và mặt phẳng (P): x + y + z + 2 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d và d' có phương trình là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa đường thẳng $d : \frac{x - 1}{1} = \frac{y + 2}{- 1} = \frac{z}{- 2}$ và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt phẳng (P)

Trong không gian Oxyz, cho hình thang cân ABCD có các đáy lần lượt là AB, CD. Biết A(3;1;-2), B(-1;3;2), C(-6;3;6), và D(a;b;c) với a, b, c $\in ℝ$ . Tính T = a+ b+ c.

Trong không gian với hệ tọa Oxyz, cho vectơ $\vec{a} = (1; - 2; 4)$ , $\vec{b} = (x_{0}; y_{0}; z_{0})$ cùng phương với vectơ $\vec{a}$ . Biết vectơ $\vec{b}$ tạo với tia Oy một góc nhọn và $|\vec{b}| = \sqrt{21}$ . Giá trị của tổng $x_{0} + y_{0} + z_{0}$ bằng