Câu hỏi:
11/07/2024 1,472
Để leo lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó, bác Dũng dịch chuyển chân thang vào gần bức tường thêm 1m thì bác Dũng nhận thấy thang tạo với mặt đất một góc 45° (Hình 21b). Bức tường cao bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
+) Hình 21a):
Đặt AC = x (m). Khi đó AB = x + 2
Xét tam giác ABC vuông tại C, có AC = x, AB = x + 2
Áp dụng định lí py – ta – go ta được:
AB2 = AC2 + BC2
⇔ (x + 2)2 = x2 + BC2
⇔ BC2 = (x + 2)2 – x2
⇔ BC2 = 4x + 4
⇔ BC = \(\sqrt {4x + 4} \)
AC là chiều cao của bức tường nên AC = DG = x.
⇒ DG = BC – 1 = \(\sqrt {4x + 4} \) - 1
Xét tam giác DGE vuông tại G, có:
tanE = \(\frac{{DG}}{{GE}}\)
⇔ tan45° = \( = \frac{x}{{\sqrt {4x + 4} - 1}}\)
⇔ 1 = \( = \frac{x}{{\sqrt {4x + 4} - 1}}\)
⇔ \(\sqrt {4x + 4} \) – 1 = x
⇔ \(\sqrt {4x + 4} \) = x + 1 (điều kiện x ≥ – 1)
⇔ x2 + 2x + 1 = 4x + 4
⇔ x2 – 2x – 3 = 0
⇔ x = 3 (thỏa mãn) và x = – 1 (không thỏa mãn)
Vậy bức tường cao 3 m.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
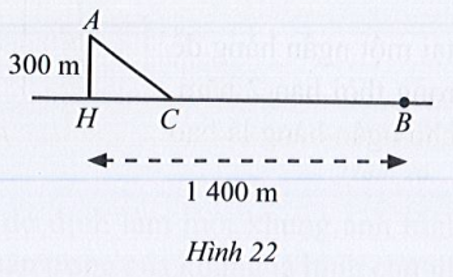
Đặt CH = x (x ≥ 0). Khi đó BC = 1 400 – x.
Xét tam giác AHC vuông tại H, có:
AH2 + HC2 = AC2
⇔ AC2 = 3002 + x2
⇔ AC = \(\sqrt {{x^2} + 90\,000} \)
Thời gian thuyền đi từ A đến C là: \(\frac{{\sqrt {{x^2} + 90\,000} }}{3}\) (giờ)
Thời gian người đi bộ đi từ B đến C là \(\frac{{1\,400 - x}}{6}\) (giờ)
Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C nên ta có:
\(\frac{{\sqrt {{x^2} + 90\,000} }}{3} = \,\frac{{1\,400 - x}}{6}\)
⇔ \(2\sqrt {{x^2} + 90\,000} = \,1400 - x\) (điều kiện x ≤ 1 400)
⇔ 4(x2 + 90 000) = 1 960 000 – 2 800x + x2
⇔ 3x2 + 2 800x – 1 600 000 = 0
⇔ x = 400 (TMĐK) hoặc x = \( - \frac{{4000}}{3}\) (không TMĐK)
⇒ CB = 1 400 – x = 1 400 – 400 = 1 000 (m).
Vậy khoảng cách CB = 1 000 m.
Lời giải
Lời giải
Đáp án đúng là D
Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)