Cho 2 hàm số $y = \frac{2}{3} x + 2; y = \frac{- 3}{2} x + 2$

a) Vẽ đồ thị hai hàm số. Tìm tọa độ giao điểm

b) Một đường thẳng song song với trục Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt đường thẳng $y = \frac{3}{2} x + 2 v à y = \frac{- 3}{2} x + 2$ tại 2 điểm M, N. Tìm tọa độ hai điểm M, .N

Xem lời giải

Câu hỏi trong đề: Bài tập theo tuần Toán 9 - Tuần 13 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Học sinh tự vẽ hai đồ thị hàm số

Ta có phương trình hoành độ giao điểm là :

$\frac{2}{3} x + 2 = - \frac{3}{2} x + 2 \Leftrightarrow \frac{13}{6} x = 0 \Rightarrow x = 0 \Rightarrow y = 2$

Vậy tọa độ giao điểm (0; 2)

b) Ta có $y_{M} = 1 \Rightarrow \frac{3}{2} x + 2 = 1 \Rightarrow x_{M} = - \frac{2}{3} \Rightarrow M (- \frac{2}{3}; 1)$

Cắt trục tung tại tung độ bằng 1 $\Rightarrow y_{N} = 1$

$\Rightarrow x_{N} = - \frac{3}{2} .1 + 2 = \frac{1}{2} \Rightarrow N (\frac{1}{2}; 1)$

Vậy $M (- \frac{2}{3}; 1); N (\frac{1}{2}; 1)$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Từ điểm A ở ngoài đường tròn (O; R), vẽ tiếp tuyến AB (B là tiếp điểm), C là điểm trên đường tròn (O) sao cho AC = AB

a) Chứng minh AC là tiếp tuyến của (O)

b) D là điểm trên AC. Đường thẳng qua C vuông góc với OD tại M. Cắt đường tròn (O) tại $E (E \neq C) .$ Chứng minh rằng DElà tiếp tuyến của (O)

Xem đáp án

Lời giải

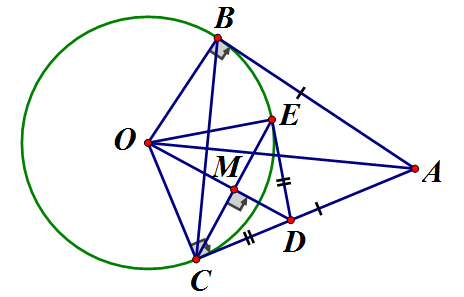
Từ điểm A ở ngoài đường tròn (O; R), vẽ tiếp tuyến AB (B là tiếp điểm), C (ảnh 1)

a) Xét $Δ O B A$ và $Δ O C A$ có: $O B = O C = R, A B = A C (g t), O A c h u n g \Rightarrow Δ O B A = Δ O C A (c . c . c)$

$\Rightarrow \hat{O C A} = \hat{O B A}$ (hai góc tương ứng) mà $\hat{O B A} = 90^{0} \Rightarrow \hat{O C A} = 90^{0}$ và $C \in (O) \Rightarrow C A$ là tiếp tuyến của (O)

b) Vì $O D ⊥ C E$ tại M $\Rightarrow$ M là trung điểm của CE $\Rightarrow O D$ là đường trung trực của CE $\Rightarrow D C = D E$

Xét $Δ O C D$ và $Δ O E D$ có $O E = O C = R; D C = D E (c m t); O D$ chung

$\Rightarrow Δ O C D = Δ O E D (c . c . c) \Rightarrow \hat{O E D} = \hat{O C D} = 90^{0}$ mà $E \in (O)$ nên ED là tiếp tuyến của (O)

Câu 2

Cho nửa đường tròn (O; R) đường kính AB. M là điểm di động trên nửa đường tròn. Qua M vẽ tiếp tuyến với nửa đường tròn. Gọi D, C lần lượt là hình chiếu của A, B trên tiếp tuyến ấy.

a) Chứng minh rằng AD + BC không đổi

b) Xác định vị trí điểm M để diện tích tứ giác ABCD lớn nhất

Xem đáp án

Lời giải

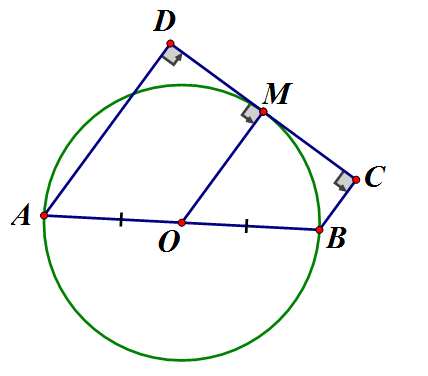
Cho nửa đường tròn (O; R) đường kính AB. M là điểm di động trên nửa đường tròn. (ảnh 1)

A D ⊥ C D (g t), B C ⊥ C D (g t), O M ⊥ C D

(CD là tiếp tuyến của (O))

$\Rightarrow A D / / B C / / O M$

Hình thang ABCD (AB // CD) có $O M / / A D / / B C, O$ là trung điểm của $A B \Rightarrow M$ là trung điểm của CD

Ta có OM là đường trung bình của hình thang $A B C D \Rightarrow \frac{A D + B C}{2} = O M$ $\Rightarrow A D + B C = 2 R$ không đổi

b) Vẽ $A E ⊥ B C$ tại E

Tứ giác ADCE có $\hat{A D C} = \hat{D C E} = \hat{C E A} = 90^{0}$ nên là hình chữ nhật $\Rightarrow C D = A E$

$A E ⊥ B C$ $\Rightarrow A E \leq A B = 2 R$

Do đó $S_{A B C D} = \frac{A D + B C}{2} . C D = R . C D \leq R .2 R = 2 R^{2}$

Nên $S_{A B C D} \leq 2 R^{2},$ không đổi

Dấu "=" xảy ra $\Leftrightarrow E \equiv B \Leftrightarrow D C / / A B \Leftrightarrow M$ là giao điểm của đường thẳng vuông góc với AB vẽ từ O và đường tròn (O)

Vậy khi M là giao điểm của đường thẳng vuông góc với OB vẽ từ (O) và đường tròn (O) thì diện tích ABCD lớn nhất

Câu 3