Thi Online Đề thi Toán lớp 6 Giữa kì 1 có đáp án
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 3)
-
6240 lượt thi
-
5 câu hỏi
-
45 phút
Câu 1:
Thực hiện phép tính (hợp lý nếu có thể):
a) 38 + 53 + 62 + 57 + 22
b) 25.15 + 47.95 + 25.38 – 47.70
c) (23.93+ 92.45) : (92.15 – 2.92)
Lời giải:
a) 38 + 53 + 62 + 57 + 22
= (38 + 62) + (53 + 57) + 22
= 100 + 110 + 22
= 232
b) 25.15 + 47.95 + 25.38 – 47.70
= 25.15 + 25.38 + 47.95 – 47.70
= 25.(15 + 38) + 47.(95 – 70)
= 25.53 + 47.25
= 25.(53 + 47)
= 25.100
= 2500
c) (23.93+ 92.45) : (92.15 – 2.92)
= (23.93+ 92.9.5) : [92.(15 – 2)]
= (23.93+ 93.5) : [92.(15 – 2)]
= [93.(23+ 5)] : (92.13)
= (93.13) : (92.13)
= 9
Câu 2:
Tìm số tự nhiên x, biết:
a) 2x + 4 = 23
b) 3x + 1 + 23 = 2.52.20220
c) 180 ⁝ x và 12 < x ≤ 20
Lời giải:
a) 2x + 4 = 23
2x = 23 – 4
2x = 19
x = 19 : 2
x = 9,5
Vậy x = 9,5.
b) 3x + 1 + 23 = 2.52.20220
3x + 1 + 23 = 50
3x + 1= 50 – 23
3x + 1= 27
3x + 1= 33
x + 1 = 3
x = 3 – 1
x = 2
Vậy x = 2.
c) 180 ⁝ x và 12 < x ≤ 20
180 ⁝ x
nên x ∈ Ư(180) = {1; 2; 3; 4; 5; 6; 9; 10; 12; 15; 18; 20; 30; 36; 45; 60; 90; 180}
Mà 12 < x ≤ 20
Nên x ∈ {15; 18; 20}
Vậy x ∈ {15; 18; 20} thì 180 ⁝ x và 12 < x ≤ 20.
Câu 3:
Cô giáo chủ nhiệm lớp 6A muốn chia 240 cuốn vở, 72 bút, 168 tập giấy kiểm tra thành một số phần thưởng như nhau để thưởng cho học sinh có thành tích cao nhân dịp sơ kết đợt thi đua chào mừng ngày 20 - 11. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó, mỗi phần thưởng có bao nhiêu cuốn vở, bút, tập giấy kiểm tra?
Lời giải:
Gọi số phần thưởng là x. \(\left( {x \in {\mathbb{N}^*}} \right)\)
Để chia 240 cuốn vở, 72 bút, 168 tập giấy kiểm tra thành một số phần thưởng như nhau và số phần thưởng nhiều nhất thì x = ƯCLN(240, 72, 168)
240 = 24.3.5
72 = 23.32
168 = 23.3.7
ƯCLN(240, 72, 168) = 23.3 = 24 hay x = 24 (t/m)
Vậy có thể chia thành 24 phần thưởng.
Mỗi phần thưởng có số cuốn vở là:
240 : 24 = 10 (cuốn vở)
Mỗi phần thưởng có số bút là:
72 : 24 = 3 (bút)
Mỗi phần thưởng có số tập giấy kiểm tra là:
168 : 24 = 7 (tập giấy)
Câu 4:
Một tòa tháp có đáy là hình lục giác đều ABCDEF.
a) Kể tên 2 hình tam giác đều, 2 hình thoi, 2 hình chữ nhật có trong hình bên.
b) Tính tổng diện tích hình chữ nhật ABDE và hình thoi AOEF theo đơn vị mét vuông. Cho AB = 90 cm; AE = 156 cm.
Lời giải:
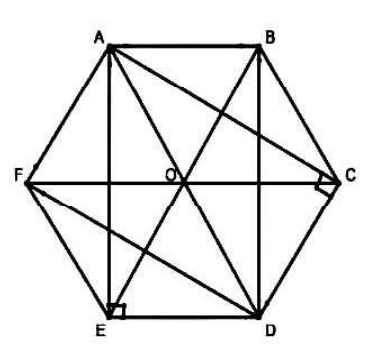
a) Hai hình tam giác đều là: tam giác đều AOB; tam giác đều BOC.
Hai hình thoi là: hình thoi AOEF; hình thoi BODC.
Hai hình chữ nhật là: hình chữ nhật ACDF; hình chữ nhật ABDE.
b) 90 cm = 0,9 m
156 cm = 1,56 m
Diện tích hình chữ nhật ABDE là:
1,56.0,9 = 1,404 (m2)
Do ABOF là hình thoi nên OF = AB = 0,9 m.
Diện tích hình thoi AOEF là:
\(\frac{1}{2}\).0,9.1,56 = 0,702 (m2)
Vậy tổng diện tích hình chữ nhật ABDE và hình thoi AOEF là:
1,404 + 0,702 = 2,106 (m2).
Câu 5:
Chứng tỏ rằng với mọi số tự nhiên n thì n2+ n + 1 là số lẻ.
Lời giải:
Ta có: n2+ n + 1 = (n . n + n) + 1 = n(n + 1) + 1
Vì n và n + 1 là hai số tự nhiên liên tiếp nên trong hai số n và n + 1, có một số là số chẵn.
TH1: n là số chẵn nên n ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
TH2: n + 1 là số chẵn nên (n + 1) ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
Do vậy trong mọi trường hợp thì n(n + 1) đều chia hết cho 2 nên nó là số chẵn, mà 1 là số lẻ nên n(n + 1) + 1 là số lẻ.
Vậy với mọi số tự nhiên n thì n2+ n + 1 là số lẻ.
Bài thi liên quan:
Đề thi Toán lớp 6 Giữa kì 1 có đáp án (Đề 1)
9 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 2)
13 câu hỏi 30 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 4)
32 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 5)
20 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 6)
12 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 7)
6 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 8)
20 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 9)
20 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 10)
20 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 11)
20 câu hỏi 45 phút
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 11)
20 câu hỏi 45 phút
Các bài thi hot trong chương:
( 5.2 K lượt thi )
( 2.6 K lượt thi )
Đánh giá trung bình
50%
0%
50%
0%
0%
Nhận xét
2 năm trước
Võ Thiện Nhân
8 tháng trước
Gia Linh Nguyễn Hoàng