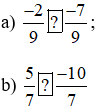20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 24: So sánh phân số. Hỗn số dương có đáp án
39 người thi tuần này 4.6 2.6 K lượt thi 19 câu hỏi 30 phút
🔥 Đề thi HOT:
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
10 Bài tập Các bài toán thực tế về số nguyên âm (có lời giải)
13 Bài tập Một số bài toán thực tế về hình vuông, hình chữ nhật (có lời giải)
Đề kiểm tra giữa kì 1 Toán 6 Cánh diều có đáp án (Đề 1)
13 Bài tập Tính chu vi và diện tích của hình bình hành, hình thang cân (có lời giải)
10 Bài tập Ứng dụng bội chung và bội chung nhỏ nhất để giải các bài toán thực tế (có lời giải)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Trong tình huống trên ta cần so sánh hai phân số và
Sau bài học này sẽ giúp chúng ta so sánh hai phân số trên.
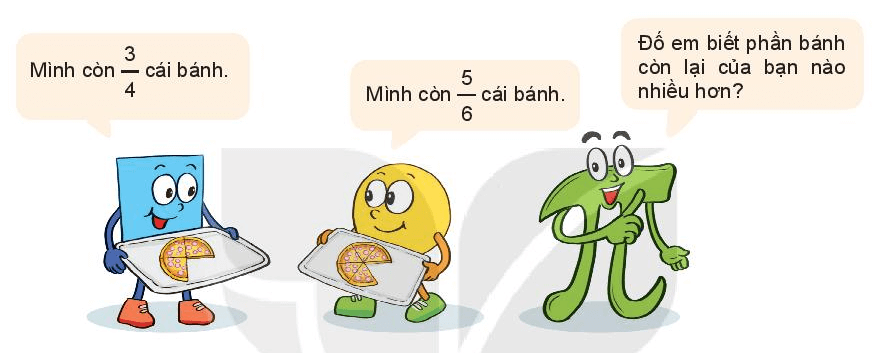
Lời giải
+) Phân tích các số 6 và 4 ra thừa số nguyên tố, ta được:
6 = 2. 3; 4 =
+) Ta thấy thừa số chung là 2; thừa số riêng là 3
+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 1
Khi đó BCNN(6; 4) = .3 = 12
Ta chọn mẫu chung của hai phân số là 12.
Ta có: (tính chất cơ bản của phân số)
(tính chất cơ bản của phân số)
Lời giải
+) Phân tích các số 5 và 2 ra thừa số nguyên tố, ta được:
5 = 5; 2 = 2
+) Ta thấy không có thừa số chung; thừa số riêng là 2 và 5
+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 5 là 1
Khi đó BCNN(5, 2) = 2. 5 = 10
Ta chọn mẫu chung của hai phân số là 10.
Ta có: (tính chất cơ bản của phân số)
(tính chất cơ bản của phân số)
Lời giải
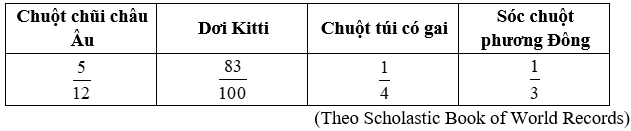
+) Ta có: 4 = ; 9 = ; 3 = 3. Do đó BCNN(4; 9; 3) = = 4.9 = 36
+) Tìm thừa số phụ: 36: 4 = 9; 36: 9 = 4 và 36: 3 = 12
+) Ta có:; ;
Lời giải
+) Quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương) thì phân số nào có tử lớn hơn thì phân số đó lớn hơn.
+) Vì 7 < 9 nên
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.