Câu hỏi:
12/07/2024 3,328
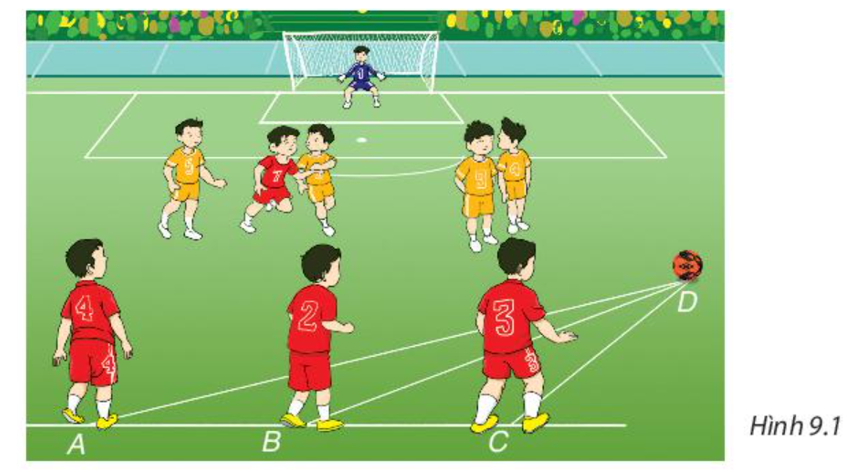
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.7). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
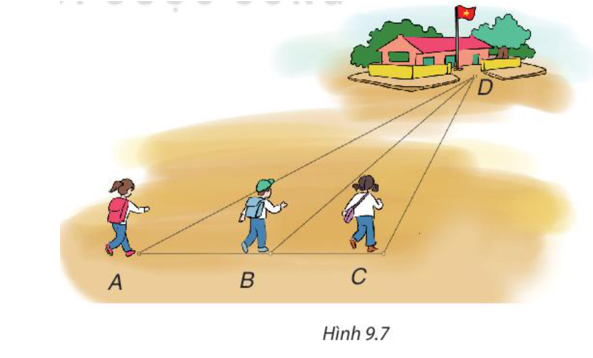
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.7). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có là góc ngoài tại đỉnh B của nên .
Do đó là góc tù.
Xét có là góc tù nên DABD là tam giác tù
Suy ra cạnh AD đối diện với là cạnh lớn nhất trong .
Khi đó AD > BD (1).
Xét DBCD có là góc tù nên DBCD là tam giác tù
Suy ra cạnh BD đối diện với là cạnh lớn nhất của DBCD.
Cạnh đối diện với trong là cạnh BD.
Do đó cạnh BD là cạnh lớn nhất trong .
Khi đó BD > CD (2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy bạn Mai đi xa nhất, bạn Hà đi gần nhất
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Ba địa điểm A, B, C là ba đỉnh của một tam giác ABC với tù, AC = 500 m. Đặt một loa truyền thanh tại một điểm nằm giữa A và B thì tại C có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500 m?
Ba địa điểm A, B, C là ba đỉnh của một tam giác ABC với tù, AC = 500 m. Đặt một loa truyền thanh tại một điểm nằm giữa A và B thì tại C có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500 m?
Xem đáp án »
12/07/2024
8,662
Câu 2:
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em, cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao? (Biết rằng góc ACD là góc tù).
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em, cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao? (Biết rằng góc ACD là góc tù).
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Xem đáp án »
12/07/2024
4,128
Câu 3:
Trong tam giác cân có một góc bằng 96o, hỏi cạnh lớn nhất của tam giác cân đó là cạnh bên hay cạnh đáy? Vì sao?
Trong tam giác cân có một góc bằng 96o, hỏi cạnh lớn nhất của tam giác cân đó là cạnh bên hay cạnh đáy? Vì sao?
Xem đáp án »
12/07/2024
3,963
Câu 4:
Trong Hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?
a) .
b)
c)
Trong Hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?
a) .
b)
c)
Xem đáp án »
12/07/2024
3,702
Câu 5:
Cho tam giác MNP có độ dài các cạnh: MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.
Cho tam giác MNP có độ dài các cạnh: MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.
Xem đáp án »
12/07/2024
3,438
Câu 6:
Cho tam giác MNP có = 47o, = 53o. Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Cho tam giác MNP có = 47o, = 53o. Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Xem đáp án »
12/07/2024
2,376
về câu hỏi!