Câu hỏi:
13/07/2024 1,724
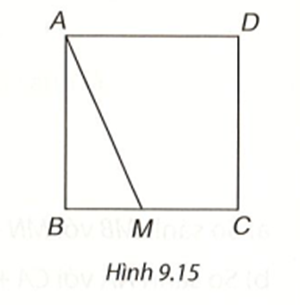
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Câu hỏi trong đề: Giải VTH Toán 7 KNTT Luyện tập chung trang 70 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi M trùng với B (hoặc D) thì AM = a (AB = a) với a là độ dài cạnh hình vuông. Khi M khác B, M thuộc cạnh BC thì tam giác ABM vuông tại B nên AM là cạnh huyền, do đó a = AB < AM. Tương tự, khi M khác D, M thuộc cạnh CD, ta có a = AD < AM.
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới)
Đã bán 230
₫ 235.000
₫ 120.000
Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới)
Đã bán 361
₫ 245.000
₫ 126.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao?
Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao?
Xem đáp án »
13/07/2024
3,656
Câu 2:
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm.
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm.
Xem đáp án »
13/07/2024
2,232
Câu 3:
Độ dài hai cạnh của một tam giác bằng 7 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Độ dài hai cạnh của một tam giác bằng 7 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Xem đáp án »
13/07/2024
1,537
Câu 4:
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Xem đáp án »
13/07/2024
1,234
Câu 5:
Cho tam giác ABC, điểm M nằm giữa B và C. Chứng minh rằng:
\(\frac{1}{2}\)(AB – BC + CA) < AM.
Cho tam giác ABC, điểm M nằm giữa B và C. Chứng minh rằng:
\(\frac{1}{2}\)(AB – BC + CA) < AM.
Xem đáp án »
13/07/2024
902
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận