Cho nửa đường tròn đường kính AB trên đó có một điểm M. Trên đường kinh AB lấy một điểm C sao cho . Trên nửa mặt phằng bờ AB có chứa điểm M, người ta kẻ các tia Ax, By vuông góc với AB; đường thẳng qua M vuông góc với MC cắt Ax tại P; đường thẳng qua C vuông góc với CP cắt By tại Q. Gọi D là giao điểm của CP và AM; E là giao điểm của CQ và BM
a) Chứng minh rằng các tứ giác ACMP, CDME nội tiếp được
Cho nửa đường tròn đường kính AB trên đó có một điểm M. Trên đường kinh AB lấy một điểm C sao cho . Trên nửa mặt phằng bờ AB có chứa điểm M, người ta kẻ các tia Ax, By vuông góc với AB; đường thẳng qua M vuông góc với MC cắt Ax tại P; đường thẳng qua C vuông góc với CP cắt By tại Q. Gọi D là giao điểm của CP và AM; E là giao điểm của CQ và BM
a) Chứng minh rằng các tứ giác ACMP, CDME nội tiếp được
Quảng cáo
Trả lời:
Giải bởi Vietjack
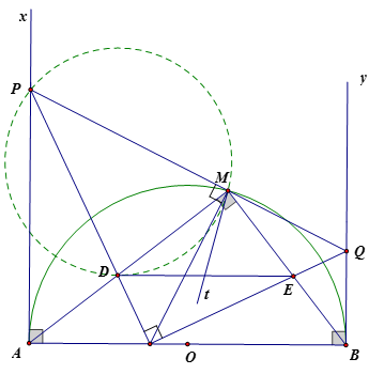
Tứ giác CDME có nên nội tiếp được
Đang tải chế độ Học...
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
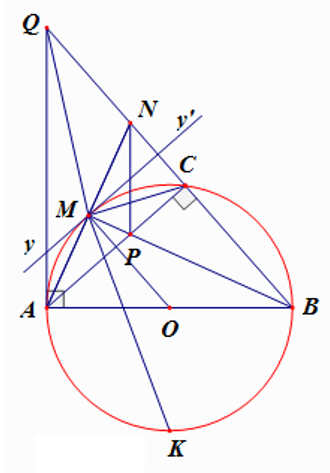
Lời giải
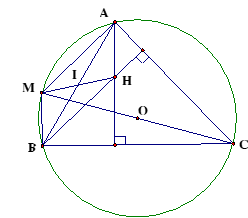
, (suy từ giả thiết).
.
Mà (cùng vuông góc với AC).
là hình bình hành.
cắt MH tại trung điểm I của AB và MH (t/c hình bình hành).
Suy ra H, I, M thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập