Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA ta lấy theo thứ tự các điểm E,F,G,H sao cho AE = BF = CG = DH . Xác định vị trí của các điểm E, F,G,H sao cho tứ giác EFGH có chu vi nhỏ nhất .
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA ta lấy theo thứ tự các điểm E,F,G,H sao cho AE = BF = CG = DH . Xác định vị trí của các điểm E, F,G,H sao cho tứ giác EFGH có chu vi nhỏ nhất .
Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!
Quảng cáo
Trả lời:
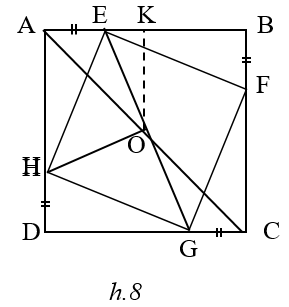
Tam giác HAE = tam giác EBF = tam giác FCG = tam giác GHD
HE = EF = FG = GH
EFGH là hình thoi .
EFGH là hình vuông
Gọi O là giao điểm của AC và EG . Tứ giác AECG có AE = CG, AE //CG nên là hình bình hành suy ra O là trung điểm của AC và EG , do đó O là tâm của cả hai hình vuông ABCD và EFGH.
DHOE vuông cân : HE2 = 2OE2 HE = OE
Chu vi EFGH = 4HE = 4 OE . Do đó chu vi EFGH nhỏ nhất OE nhỏ nhất
Kẻ OK vuông góc với AB OE ≥OK ( OK không đổi )
OE = OK E ≡ K
Do đó min OE = OK
Như vậy, chu vi tứ giác EFGH nhỏ nhất khi và chỉ khi E,F,G,H là trung điểm của AB , BC, CD, DA.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
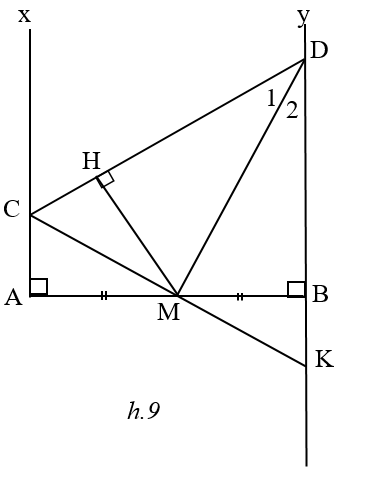
Gọi K là giao điểm của CM và DB
MA = MB ; ,
Tam giác MAC = MBK MC = MK
Mặt khác DM vuông góc với CK
tam giác DCK cân
Kẻ MH vuông góc với CD .
Tam giác MHD = MBD MH = MB = a
SMCD =CD.MH ≥ AB.MH = 2a.a= a2
SMCD = a2 CD vuông góc với Ax khi đó = 450 ; =450.
Vậy min SMCD = a2 . Các điểm C,D được xác định trên Ax; By sao cho AC = BD =a .
Lời giải
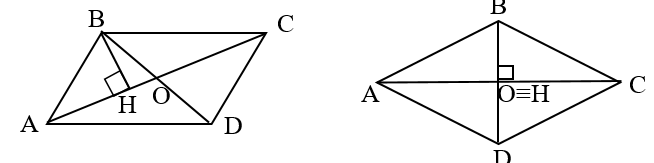
Xét hình bình hành ABCD có AC = 8 cm; BD = 6 cm ( h.6)
Gọi O là giao điểm hai đường chéo. Kẻ BH vuông góc với AC .
Ta có : SABCD = 2SABC = AC.BH
Ta có AC = 8cm, BH ≤ BO = 3cm. Do đó :
SABCD ≤ 8.3 = 24 (cm2)
SABCD = 24 cm2 BH ≡ BO H ≡ O BD vuông góc với AC
Vậy max SABCD = 24 cm2 . Khi đó hình bình hành ABCD là hình thoi (h.7) có diện tích 24cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.