Cho nửa đường tròn đường kính BC = 2R. Từ điểm A trên nửa đường tròn vẽ AH vuông góc với BC Nửa đường tròn đường kính BH, CH lần lượt có tâm O₁; O₂ cắt AB, AC thứ tự tại D và E.
Xác định vị trí điểm A để diện tích tứ giác $D E O_{1} O_{2}$ đạt giá trị lớn nhất. Tính giá trị đó.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

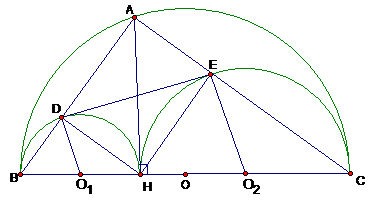
Media VietJack

Vì $O_{1} D = O_{1} B$ => $Δ O_{1} B D$ cân tại => $\hat{B} = \hat{B D O_{1}}$ (2)

Từ (1), (2) => $\hat{A D E} + \hat{B D O_{1}} = \hat{B} + \hat{B A H}$ = 900 => $O_{1} D / / O_{2} E$

Vậy là hình thang vuông tại D và E.

Ta có S = $\frac{1}{2} (O_{1} D + O_{2} E) . D E = \frac{1}{2} O_{1} O_{2} . D E \leq \frac{1}{2} O_{1} O_{2}^{2}$

(Vì $O_{1} D + O_{2} E = O_{1} H + O_{2} H = O_{1} O_{2}$ và $D E \leq O_{1} O_{2}$ )

$S_{h t} \leq \frac{1}{2} O_{1} {O_{2}}^{2} = \frac{B C^{2}}{8} = \frac{R^{2}}{2}$

Dấu "=" xảy ra khi và chỉ khi $D E = O_{1} O_{2}$

$\Leftrightarrow D E O_{1} O_{2}$ là hình chữ nhật

$\Leftrightarrow$ A là điểm chính giữa cung BC Khi đó max $S_{D E O_{1} O_{2}} = \frac{R^{2}}{2}$ .

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.

Chứng minh AB là tiếp tuyến của đường tròn đường kính CD

Xem đáp án

Lời giải

Media VietJack

Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD có IO là bán kính.

Theo tính chất tiếp tuyến ta có AC ^ AB; BD ^ AB => AC // BD => tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB => IO là đường trung bình của hình thang ACDB

IO // AC, mà AC ^ AB => IO ^ AB tại O => AB là tiếp tuyến tại O của đường tròn đường kính CD

Câu 2

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N.

Chứng minh $\hat{C O D} = 90^{0}$ .

Xem đáp án

Lời giải

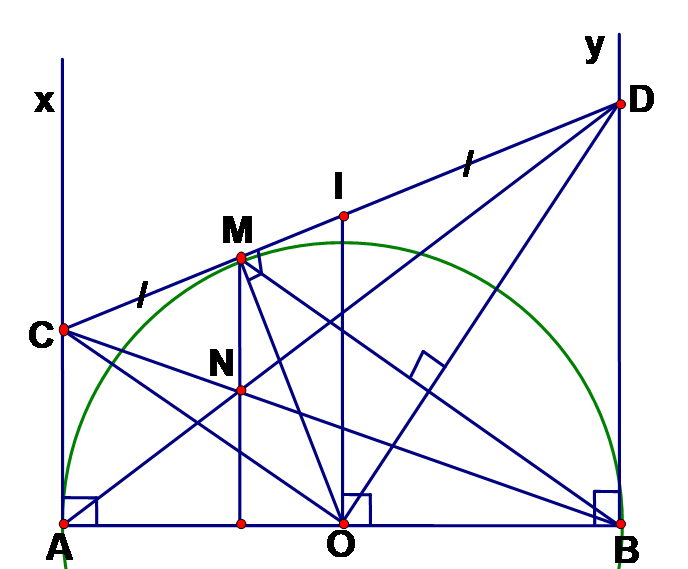
Media VietJack

Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là tia phân giác của góc AOM; OD là tia phân giác của góc BOM, mà $\hat{A O M}$ và $\hat{B O M}$ là hai góc kề bù => $\hat{C O D}$ = 900.

Câu 3