Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)

Giả sử A, B, I cố định. Hãy xác định vị trí của điểm C sao cho diện tích tứ giác ABKI lớn nhất.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

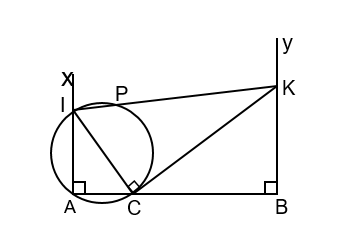
Media VietJack

Từ giả thiết suy ra tứ giác AIKB là hình thang vuông, gọi s là diện tích của AIKB, khi đó ta có: . Dễ thấy s lớn nhất khi và chỉ khi KB lớn nhất (do A, B, I cố định).

Xét các tam giác vuông AIC và BKC có: và suy ra: (góc có cạnh tương ứng vuông góc) hay đồng dạng với (g-g).

Suy ra: $\frac{A C}{B K} = \frac{A I}{B C} \Leftrightarrow B K = \frac{A C . B C}{A I}$ , khi đó: BK lớn nhất ACBC lớn nhất

Theo BĐT Côsi có: $A C . C B \leq {(\frac{A C + C B}{2})}^{2} = \frac{A B^{2}}{4}$ , dấu “=” xảy ra khi và chỉ khi C là trung điểm của AB Vậy diện tích tứ giác AIBK lớn nhất khi và chỉ khi C là trung điểm của AB

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.

Chứng minh AB là tiếp tuyến của đường tròn đường kính CD

Xem đáp án

Lời giải

Media VietJack

Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD có IO là bán kính.

Theo tính chất tiếp tuyến ta có AC ^ AB; BD ^ AB => AC // BD => tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB => IO là đường trung bình của hình thang ACDB

IO // AC, mà AC ^ AB => IO ^ AB tại O => AB là tiếp tuyến tại O của đường tròn đường kính CD

Câu 2

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.

Chứng minh MN ^ AB

Xem đáp án

Lời giải

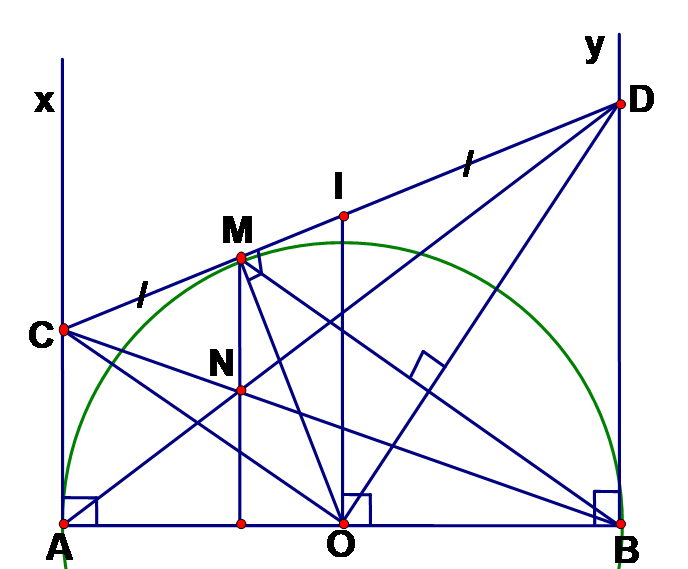
Media VietJack

Theo trên AC // BD => , mà CA = CM; DB = DM nên suy ra => MN // BD mà BD ^ AB => MN ^ AB

Câu 3