Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Trong tam giác ABC, (Hình 9):
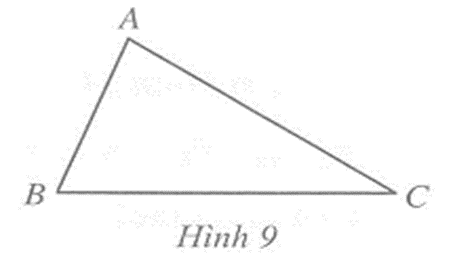
+ Góc A được gọi là góc đối diện với cạnh…., góc B được gọi là góc đối diện với cạnh…, góc C được gọi là góc đối diện với cạnh…..
+ Cạnh BC được gọi là cạnh đối diện với góc…., cạnh CA được gọi là cạnh đối diện với góc…., cạnh AB được gọi là cạnh đối diện với góc……
- Trong một tam giác
+ Góc đối diện với cạnh lớn hơn là góc …. hơn.
+ Cạnh đối diện với góc lớn hơn là cạnh …. hơn.
Nhận xét: Trong tam giác vuông, cạnh …. là cạnh lớn nhất
Trong tam giác tù, cạnh đối diện với góc …. là cạnh lớn nhất
Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Trong tam giác ABC, (Hình 9):
+ Góc A được gọi là góc đối diện với cạnh…., góc B được gọi là góc đối diện với cạnh…, góc C được gọi là góc đối diện với cạnh…..
+ Cạnh BC được gọi là cạnh đối diện với góc…., cạnh CA được gọi là cạnh đối diện với góc…., cạnh AB được gọi là cạnh đối diện với góc……
- Trong một tam giác
+ Góc đối diện với cạnh lớn hơn là góc …. hơn.
+ Cạnh đối diện với góc lớn hơn là cạnh …. hơn.
Nhận xét: Trong tam giác vuông, cạnh …. là cạnh lớn nhất
Trong tam giác tù, cạnh đối diện với góc …. là cạnh lớn nhất
Quảng cáo
Trả lời:
Giải bởi Vietjack
+ Góc A được gọi là góc đối diện với cạnh BC, góc B được gọi là góc đối diện với cạnh AC, góc C được gọi là góc đối diện với cạnh AB.
+ Cạnh BC được gọi là cạnh đối diện với góc A, cạnh CA được gọi là cạnh đối diện với góc B, cạnh AB được gọi là cạnh đối diện với góc C
- Trong một tam giác
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn.
+ Cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Nhận xét: Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
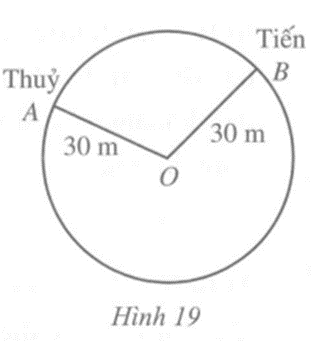
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ đến bán kính 100 km. Người ta đặt một trạm phát sóng mạnh 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 25 km (Hình 15). Sóng 4G của trạm phát sóng tại vị trí A có thể phủ đến đảo đó được không? Vì sao?
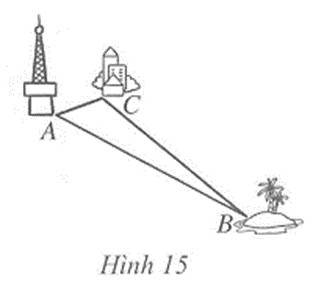
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ đến bán kính 100 km. Người ta đặt một trạm phát sóng mạnh 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 25 km (Hình 15). Sóng 4G của trạm phát sóng tại vị trí A có thể phủ đến đảo đó được không? Vì sao?
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có AC = 20 (km), BC = 75 (km)
Suy ra AC + BC = 20 + 75 = 95 (km)
Vì AB < BC + AC (bất đẳng thức tam giác) nên AB < 95 (km).
Do AB < 95 (km) và sóng 4G phủ đến bán kính 100 km nên sóng 4G của trạm phát sóng tại vị trí A có phủ đến đảo đó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trong một tam giác, tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại.
Đối với tam giác ABC, ta có AB + BC > AC, AB + AC > BC, AC + BC > AB
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập