Câu hỏi:
22/02/2023 332
Có một mô hình kim tự tháp là một chóp tứ giác đều có cạnh bằng 6cm; cạnh đáy bằng 4cm được đặt trên một bàn trưng bày (đáy nằm trên mặt bàn). Một chú kiến tinh nghịch đang ở đỉnh của đáy và có ý định khám phá một vòng qua tất cả các mặt và trở về vị trí ban đầu. Tính quãng đường ngắn nhất của chú kiến (nếu kết quả lẻ thì làm tròn đến 2 chữ số thập phân).
Có một mô hình kim tự tháp là một chóp tứ giác đều có cạnh bằng 6cm; cạnh đáy bằng 4cm được đặt trên một bàn trưng bày (đáy nằm trên mặt bàn). Một chú kiến tinh nghịch đang ở đỉnh của đáy và có ý định khám phá một vòng qua tất cả các mặt và trở về vị trí ban đầu. Tính quãng đường ngắn nhất của chú kiến (nếu kết quả lẻ thì làm tròn đến 2 chữ số thập phân).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Trải tất cả các mặt bên của khối chóp ra cùng một mặt phẳng.
Cách giải:
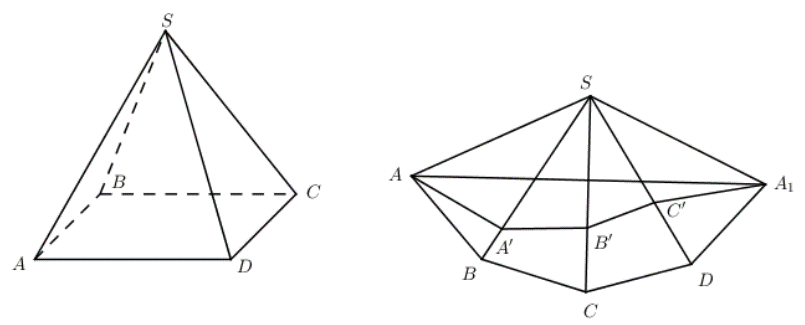
Trải hình chóp S.ABCD trên cùng một mặt phẳng \(\left( {{A_1} \equiv A} \right)\)
Giả sử quãng đường của con kiến đi từ A đến \({A_1}\) là , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn \(A{A_1}\)
Xét tam giác SAB có:
\(\cos \angle ASB = \frac{{S{A^2} + S{B^2} - A{B^2}}}{{2SA.SB}} = \frac{{{6^2} + {6^2} - {4^2}}}{{{{2.6}^2}}} = \frac{7}{9}\)
\( \Rightarrow \angle ASB \approx 38,{9^0}\)
\( \Rightarrow \angle AS{A_1} = 4\angle ASB = 155,{8^0}\)
Xét tam giác \(AS{A_1}\) có:
\[{\rm{AA}}_1^2 = S{A^2} + SA_1^2 - 2SA.S{A_1}.{{\mathop{\rm cosASA}\nolimits} _1} \approx 11,73\left( {cm} \right)\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Phương pháp:
+) Gọi hai điểm A, B thuộc đồ thị hàm số, lưu ý điều kiện nằm ở hai nhánh khác nhau.
+) Tính AB, sử dụng BĐT Cauchy để tìm GTNN của AB.
Cách giải:
TXĐ: \(D = R\backslash \left\{ { - 1} \right\}\)
Ta có: \(y = \frac{{2x - 1}}{{x + 1}} = 2 - \frac{3}{{x + 1}}\)
Đồ thị hàm số có TCĐ \(x = - 1\), gồm hai nhánh nằm về hai phía đường thẳng \(x = - 1\).
Gọi A là điểm thuộc nhánh trái của đồ thị hàm số \( \Rightarrow {x_A} < - 1 \Rightarrow - 1 - {x_A} > 0\)
Đặt \(a = - 1 - {x_A} > 0 \Rightarrow {x_A} = - 1 - a \Rightarrow A\left( { - 1 - a;2 + \frac{3}{a}} \right)\)
Gọi B là điểm thuộc nhánh phải của đồ thị hàm số \( \Rightarrow {x_B} > - 1 \Rightarrow {x_B} + 1 > 0\)
Đặt \(b = 1 + {x_B} > 0 \Rightarrow {x_B} = - 1 + b \Rightarrow B\left( { - 1 + b;2 - \frac{3}{b}} \right)\)
\( \Rightarrow A{B^2} = {\left( {a + b} \right)^2} + {\left( {\frac{3}{b} + \frac{3}{a}} \right)^2} = {\left( {a + b} \right)^2} + \frac{{9{{\left( {a + b} \right)}^2}}}{{{a^2}{b^2}}} = {\left( {a + b} \right)^2}\left( {1 + \frac{9}{{{a^2}{b^2}}}} \right) = \left( {{a^2} + {b^2} + 2ab} \right)\left( {1 + \frac{9}{{{a^2}{b^2}}}} \right)\) Áp dụng BĐT Cauchy ta có \(A{B^2} \ge \left( {2ab + 2ab} \right).2\sqrt {\frac{9}{{{a^2}{b^2}}}} = 4ab.2.\frac{3}{{ab}} = 24 \Rightarrow AB \ge 2\sqrt 6 \)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b > 0\\1 = \frac{3}{{ab}}\end{array} \right. \Leftrightarrow a = b = \sqrt 3 \)
Vậy \(A{B_{\min }} = 2\sqrt 6 \)
Lời giải
Đáp án B
Phương pháp:
Đưa về cùng cơ số.
Cách giải:
ĐK: \(\left\{ \begin{array}{l}x + 2 > 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 2\\x > 0\end{array} \right. \Leftrightarrow x > 0\)
\({\log _4}\left( {x + 2} \right) = {\log _2}x \Leftrightarrow {\log _{{2^2}}}\left( {x + 2} \right) = {\log _2}x\)
\( \Leftrightarrow {\log _2}\sqrt {x + 2} = {\log _2}x \Leftrightarrow \sqrt {x + 2} = x\)
\( \Leftrightarrow x + 2 = {x^2} \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {tm} \right)\\x = - 1\left( {ktm} \right)\end{array} \right.\)
Vậy phương trình có nghiệm duy nhất \(x = 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận