Câu hỏi:
22/02/2023 477
Cho hình chóp S.ABCD, M là trung điểm của SA. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (ABCD). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai khối gồm khối chứa điểm S có thể tích \({V_1}\) và khối chứa điểm A có thể tích \({V_2}\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
Cho hình chóp S.ABCD, M là trung điểm của SA. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (ABCD). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai khối gồm khối chứa điểm S có thể tích \({V_1}\) và khối chứa điểm A có thể tích \({V_2}\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
Đáp án chính xác
Câu hỏi trong đề:
Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng công thức tỉ số thể tích.
Cách giải:
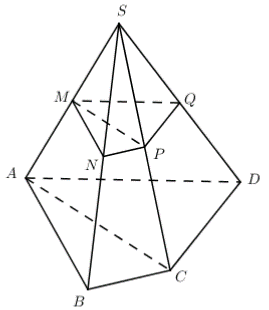
Gọi N, P, Q lần lượt là trung điểm của SB, SC, SD ta có \(\left( {MNPQ} \right)//\left( {ABCD} \right) \Rightarrow \left( {MNPQ} \right) \equiv \left( \alpha \right)\)
Ta có:
\(\frac{{{V_{SMNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}} = \frac{1}{2}.\frac{1}{2}.\frac{1}{2} = \frac{1}{8} \Rightarrow {V_{S.MNP}} = \frac{1}{8}{V_{S.ABC}}\)
\(\frac{{{V_{SMPQ}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = \frac{1}{2}.\frac{1}{2}.\frac{1}{2} = \frac{1}{8} \Rightarrow {V_{SMPQ}} = \frac{1}{8}{V_{S.ACD}}\)
\( \Rightarrow {V_1} = {V_{SMNP}} + {V_{SMPQ}} = \frac{1}{8}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \frac{1}{8}{V_{S.ABCD}}\)
\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{1}{7}\)
Chú ý và sai lầm: Công thức tỉ số thể tích chỉ áp dụng với chóp tam giác.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tính khoảng cách d giữa 2 điểm cực trị của đồ thị hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)
Tính khoảng cách d giữa 2 điểm cực trị của đồ thị hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)
Xem đáp án »
22/02/2023
2,877
Câu 2:
Phương trình \({\log _4}\left( {x + 2} \right) = {\log _2}x\) có bao nhiêu nghiệm?
Phương trình \({\log _4}\left( {x + 2} \right) = {\log _2}x\) có bao nhiêu nghiệm?
Xem đáp án »
22/02/2023
2,759
Câu 3:
Tính khoảng cách d ngắn nhất giữa hai điểm thuộc hai nhánh của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)
Tính khoảng cách d ngắn nhất giữa hai điểm thuộc hai nhánh của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)
Xem đáp án »
22/02/2023
2,653
Câu 4:
Có bao nhiêu giá trị nguyên của m để phương trình \({2^{2x + 1}} - {2^{x + 3}} - 2m = 0\) có hai nghiệm phân biệt?
Có bao nhiêu giá trị nguyên của m để phương trình \({2^{2x + 1}} - {2^{x + 3}} - 2m = 0\) có hai nghiệm phân biệt?
Xem đáp án »
22/02/2023
1,595
Câu 5:
Tìm tất cả các giá trị của tham số m để hàm số \(y = \frac{{x - 2}}{{mx - 1}}\) đồng biến trên \(\left( {1; + \infty } \right)\)
Tìm tất cả các giá trị của tham số m để hàm số \(y = \frac{{x - 2}}{{mx - 1}}\) đồng biến trên \(\left( {1; + \infty } \right)\)
Xem đáp án »
22/02/2023
1,417
Câu 6:
Tìm tất cả các giá trị m để hàm số \(y = mx + 2\sin x - 3\cos \,x\) nghịch biến trên R.
Tìm tất cả các giá trị m để hàm số \(y = mx + 2\sin x - 3\cos \,x\) nghịch biến trên R.
Xem đáp án »
22/02/2023
1,075
Câu 7:
Cho bảng biến của hàm số \(y = f\left( x \right)\) như sau:
Đồ thị của hàm số đã cho có tổng số bao nhiêu đường tiệm cận đứng và ngang?
Cho bảng biến của hàm số \(y = f\left( x \right)\) như sau:
Đồ thị của hàm số đã cho có tổng số bao nhiêu đường tiệm cận đứng và ngang?
Xem đáp án »
22/02/2023
1,000
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
120 câu Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
về câu hỏi!