Cho tam giác ABC với AB = 6 cm, AC = 9 cm.
a) Lấy điểm M, N lần lượt trên các cạnh AB, AC sao cho AM = 4 cm, AN = 6 cm. Chứng minh rằng ∆AMN ᔕ ∆ABC và tìm tỉ số đồng dạng.
b) Lấy điểm P trên cạnh AC sao cho AP = 4 cm. Chứng minh rằng ∆APB ᔕ ∆ABC.
Cho tam giác ABC với AB = 6 cm, AC = 9 cm.
a) Lấy điểm M, N lần lượt trên các cạnh AB, AC sao cho AM = 4 cm, AN = 6 cm. Chứng minh rằng ∆AMN ᔕ ∆ABC và tìm tỉ số đồng dạng.
b) Lấy điểm P trên cạnh AC sao cho AP = 4 cm. Chứng minh rằng ∆APB ᔕ ∆ABC.
Quảng cáo
Trả lời:
Lời giải
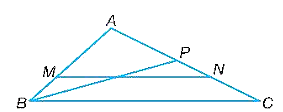
a)
Xét tam giác ABC có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\,\,\,\,\,\,\left( {do\,\,\frac{4}{6} = \frac{6}{9} = \frac{2}{3}} \right)\)
Suy ra MN song song với BC (định lí Thalès đảo)
Do ∆AMN ᔕ ∆ABC với tỉ số đồng dạng \(\frac{2}{3}\) (1).
b)
Tam giác APB và tam giác AMN có:
AP = AM (= 4 cm)
\(\widehat A\) chung
AB = AN (= 6 cm)
Do đó, ∆APB = ∆AMN (c.g.c). Suy ra ∆APB ᔕ ∆AMN (2).
Từ (1) và (2) ta có: ∆APB ᔕ ∆ABC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
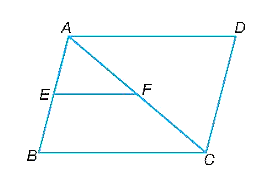
Vì ABCD là hình bình hành nên \(\widehat B = \widehat D\), AB = CD, BC = AD.
Do đó, ∆ABC = ∆CDA (c.g.c). Suy ra ∆ABC ᔕ ∆CDA (1).
Tam giác ABC có E, F lần lượt là trung điểm của AB và AC nên EF là đường trung bình tam giác ABC. Do đó, EF // BC.
Tam giác ABC có:
EF // BC nên ∆AEF ᔕ ∆ABC (2).
Từ (1) và (2) suy ra: ∆AEF ᔕ ∆CDA.
Lời giải
Lời giải
Khi viết ∆ABC ᔕ ∆MNP thì góc ABC của tam giác CBA tương ứng với góc PNM của tam giác MNP.
Ta có:
Các cặp góc tương ứng bằng nhau: \(\widehat {ABC} = \widehat {MNP},\widehat {BAC} = \widehat {NMP},\widehat {ACB} = \widehat {MPN}\);
Các cặp cạnh tương ứng tỉ lệ: \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{AC}}{{MP}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.