Quảng cáo
Trả lời:
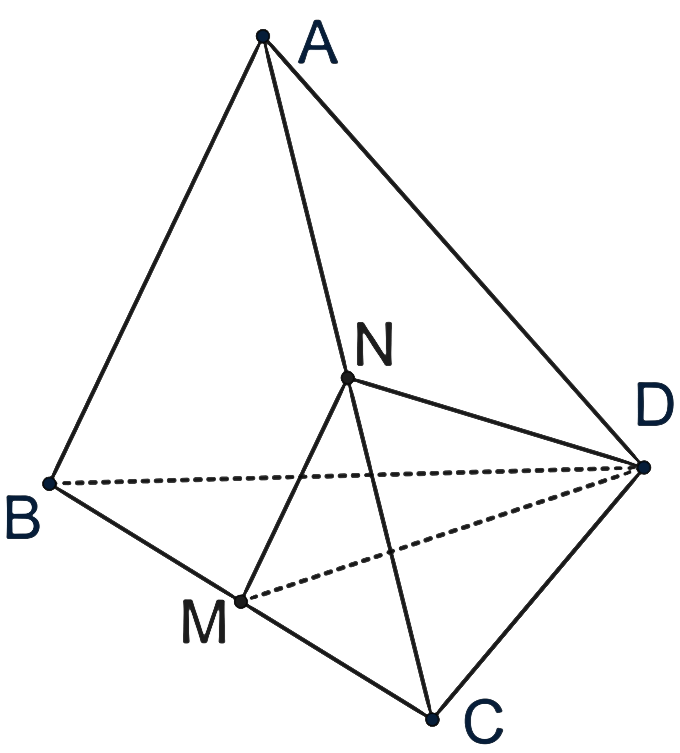
Cho N là trung điểm của cạnh AC.
Þ MN là đường trung trực của ∆ABC.
Þ MN // AB Û (AB, DM) = (MN, DM) =
Lại có: ∆BCD và ∆ACD là các tam giác đều (theo giả thiết).
Giả sử ABCD là tứ diện đều cạnh a.
Þ DM = DN = ; MN = = .
Áp dụng định lý hàm cos trong ∆DMN, ta có:
Do đó (AB, DM) = ≈ 73,22°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
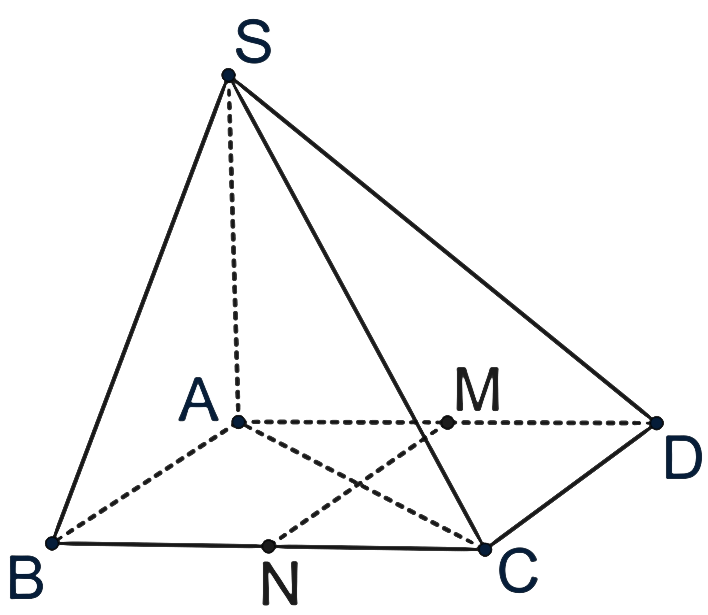
a) Ta có:
Þ SA ^ (ABCD) Û SA ^ AD.
Do BC // AD nên (BC, SD) = (AD, SD).
Do đó = 60°.
b) Do MN // CD nên (SD, MN) = (SD, CD) = .
Áp dụng định lí Pythagore, ta có:
Áp dụng định lí hàm cos trong ∆SCD, ta có:
Do đó (SD, MN) = ≈ 75,52°.
Lời giải
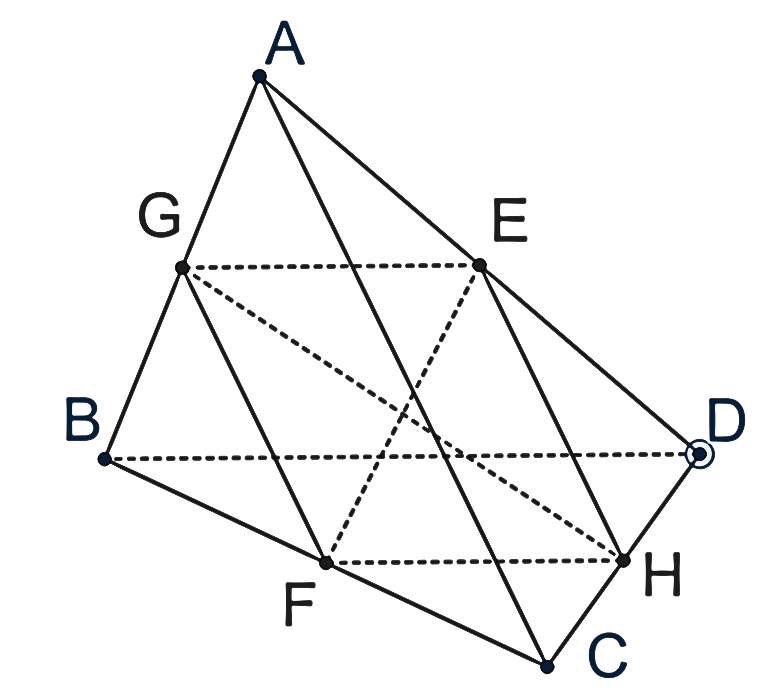
a) Gọi E, F lần lượt là trung điểm của các cạnh AD, BC.
Xét ∆BAD và ∆CDA, ta có:
Do đó ∆BAD = ∆CDA (c.c.c)
Ta có BE = CE (2 đường trung tuyến ứng với cạnh AD).
Suy ra ∆BEC cân tại E nên EF ⊥ BC.
Chứng minh tương tự, ta có: EF ⊥ AD.
Vậy đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó.
b) Gọi G, H lần lượt là các trung điểm của 2 cạnh AB và CD.
Theo tính chất đường trung bình, ta có:
Þ EH = GF = EG = HF
Khi đó, EHFG là hình thoi, suy ra EF ^ GH.
Vậy hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.