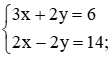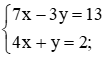Xét bài toán trong tình huống mở đầu. Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
a) Lập hệ phương trình đối với hai ẩn x, y.
b) Giải hệ phương trình nhận được ở câu a để tìm câu trả lời cho bài toán.
Xét bài toán trong tình huống mở đầu. Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
a) Lập hệ phương trình đối với hai ẩn x, y.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
– Nếu tăng thêm 8 luống, nhưng mỗi luống trồng ít đi 3 cây cải bắp thì số cải bắp của cả vườn sẽ ít đi 108 cây;
Số luống trong vườn sau khi tăng thêm 8 luống là x + 8 (luống).
Khi mỗi luống trồng ít đi 3 cây cải bắp thì số cây bắp cải ở mỗi luống là: y – 3 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x + 8)(y – 3) = xy – 108
xy – 3x + 8y – 24 = xy – 108
3x – 8y = 84. (1)
– Nếu giảm đi 4 luống, nhưng mỗi luống trồng thêm 2 cây thì số cải bắp cả vườn sẽ tăng thêm 64 cây.
Số luống trong vườn sau khi giảm đi 4 luống là x – 4 (luống).
Khi mỗi luống trồng thêm 2 cây cải bắp thì số cây bắp cải ở mỗi luống là: y + 2 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x – 4)( y + 2) = xy + 64
xy + 2x – 4y – 8 = xy + 64
2x – 4y = 72
x – 2y = 36. (2)
Từ (1) và (2) ta có hệ phương trình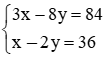 
.
Từ phương trình thứ hai, ta có x = 2y + 36. Thế vào phương trình thứ nhất, ta được
3(2y + 36) – 8y = 84, tức là 6y + 216 – 8y = 84, suy ra 2y = 132 hay y = 66.
Từ đó x = 2y + 36 = 2 . 66 + 36 = 168.
Số cây cải bắp được trồng trên mảnh vườn đó là: 168 . 66 = 11 088 (cây).
Vậy số cây cải bắp được trồng trên mảnh vườn đó là 11 088 cây.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Cộng từng vế của hai phương trình ta được 3x + 2y + 2x – 2y = 20 hay 5x = 20, suy ra x = 4.
Thế x = 4 vào phương trình thứ nhất, ta được 3 . 4 + 2y = 6 hay 2y = –6, suy ra y = –3.
Vậy hệ phương trình đã cho có nghiệm là (4; –3).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Từ phương trình thứ hai ta có y = –4x + 2. Thế vào phương trình thứ nhất, ta được
7x – 3(–4x + 2) = 13, tức là 7x + 12x – 6 = 13, suy ra 19x = 19 hay x = 1.
Từ đó y = –4 . 1 + 2 = –2.
Vậy hệ phương trình đã cho có nghiệm là (1; –2).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập