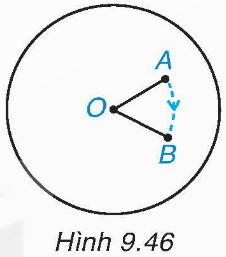
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có dạng hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay có dạng hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều quay của kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.

Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?

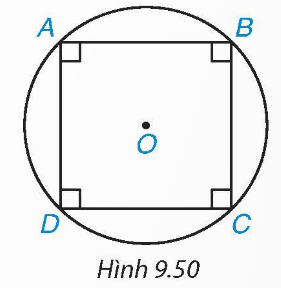
Phép quay thuận chiều 90° với tâm O biến các điểm A, B, C, D thành các điểm tương ứng là B, C, D, A.

Phép quay này giữ nguyên hình vuông ABCD.

Cách 1:

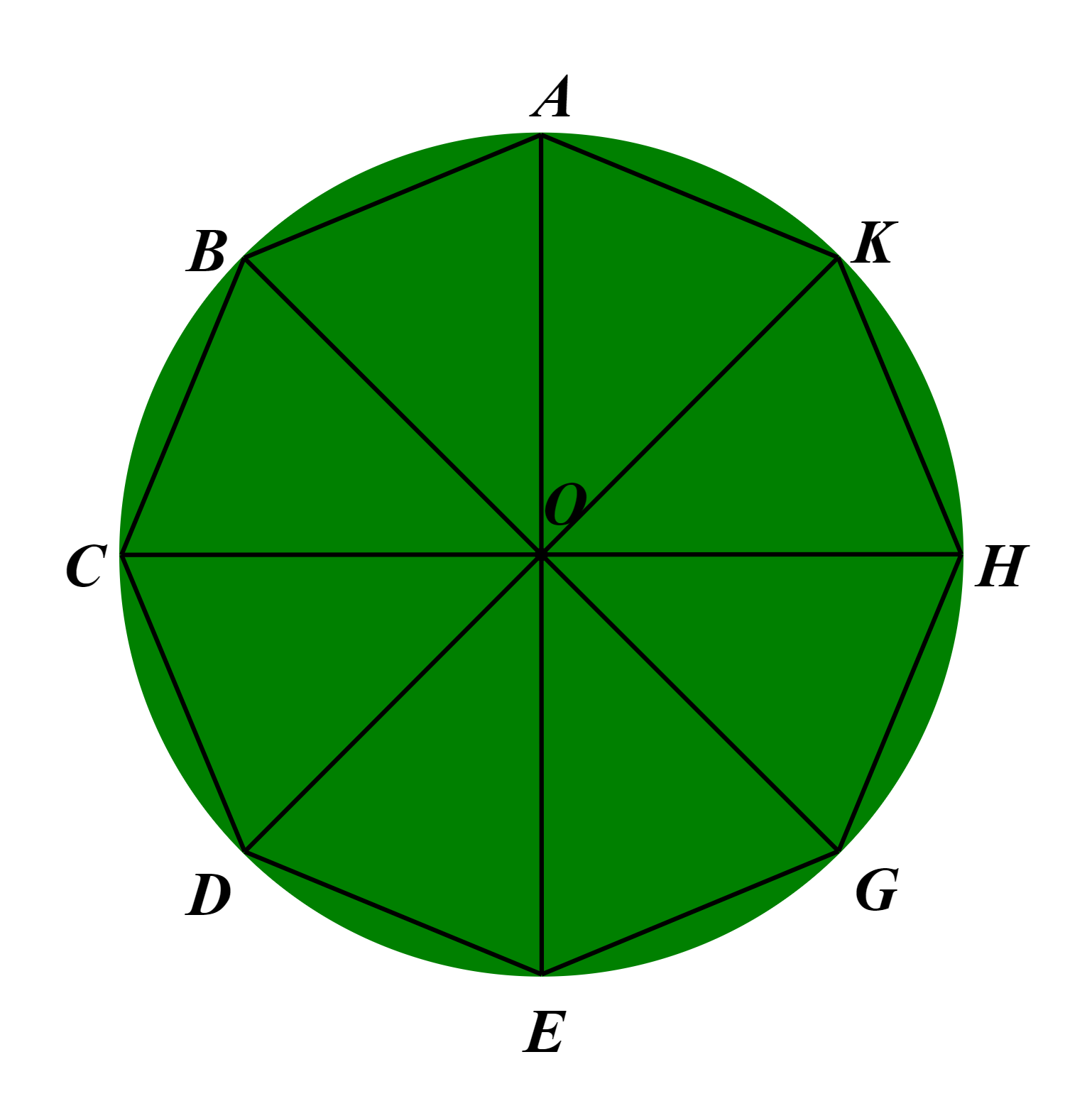
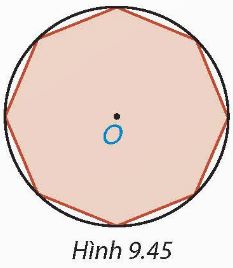
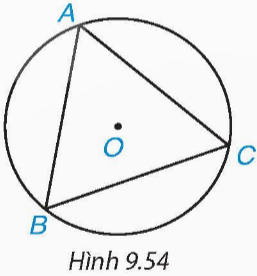
Giả sử ABCDEGHK là bát giác đều nội tiếp đường tròn (O).

Do đó AB = BC = CD = DE = EG = GH = HK và OA = OB = OC = OD = OE = OG = OH = OK.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC

Do đó ∆OAB = ∆OBC (c.c.c).

Tương tự, ta sẽ chứng minh được:

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.

Suy ra các góc tương ứng bằng nhau:

Ta có:

Suy ra nên

Lại có (tổng ba góc của ∆OAB bằng 180°)

Suy ra

Vì ∆AOB = ∆OKA nên (hai góc tương ứng).

Suy ra

Do đó, vì ABCDEGHK là bát giác đều nên các góc bằng nhau và bằng 135°.

Cách 2:

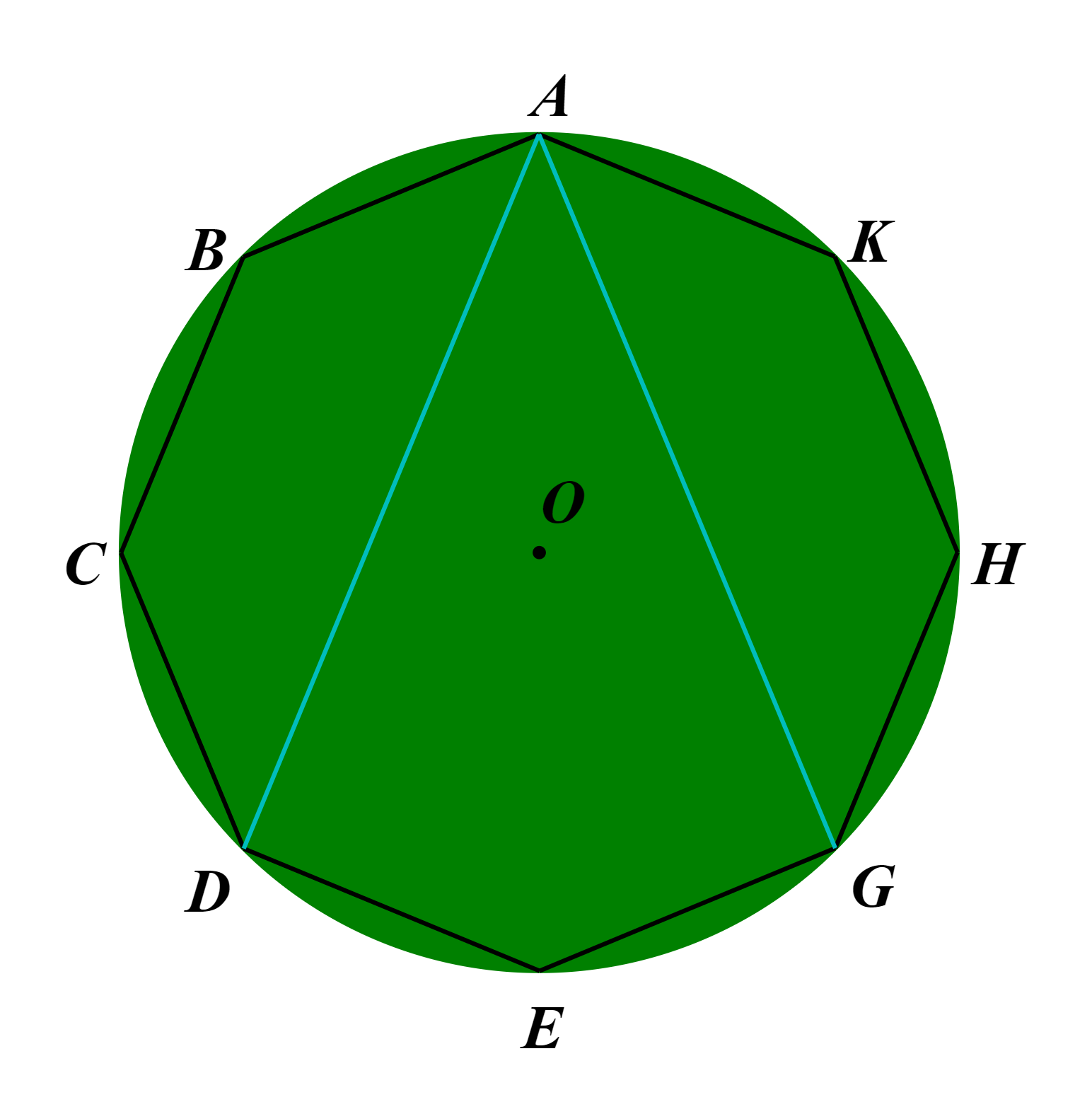
Bát giác đều ABCDEGHK được chia thành ba tứ giác ABCD, ADEG và AGHG.

Ta thấy tổng số đo các góc của bát giác ABCDEGHK bằng tổng số đo các góc của ba tứ giác kể trên.

Mà mỗi tứ giác có tổng số đo các góc bằng 360°, do đó tổng số đo các góc của bát giác đều ABCDEGHK là: 3.360° = 1 080°.

Vì ABCDEGHK là bát giác đều nên 8 góc của bát giác bằng nhau và mỗi góc có số đo bằng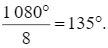

Vậy mỗi góc của bát giác đều có số đo bằng 135°.