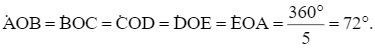Giải SGK Toán 9 KNTT Bài 30. Đa giác đều có đáp án

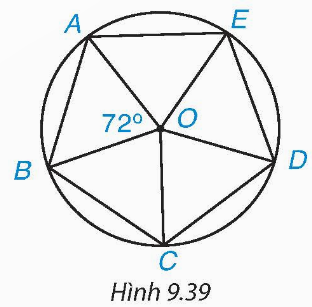
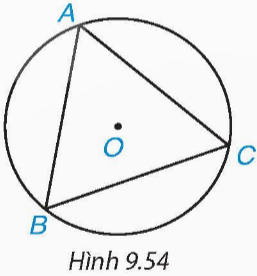
Vì năm điểm A, B, C, D, E cùng nằm trên đường tròn (O) nên OA = OB = OC = OD = OE.

Xét ∆AOB và ∆BOC có:

OA = OB, OB = OC

Do đó ∆AOB = ∆BOC (c.g.c)

Tương tự, ta sẽ chứng minh được: ∆AOB = ∆BOC = ∆COD = ∆DOE = ∆EOA.

Do đó:

⦁ AB = BC = CD = DE = EA;

⦁ 

⦁ 

Suy ra

Hay

Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.

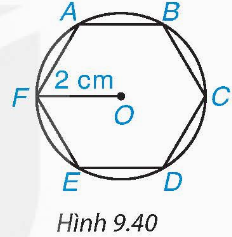
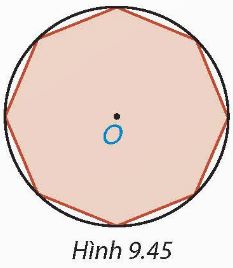
Vì ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.

Vì lục giác đều ABCDEF nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OF.

Xét ∆AOB và ∆BOC có:

OA = OB, OB = OC, AB = BC.

Do đó ∆AOB = ∆BOC (c.c.c)

Tương tự, ta sẽ chứng minh được:

∆AOB = ∆BOC = ∆COD = ∆DOE = ∆EOF = ∆OFA.

Do đó:

Mà

Suy ra nên

Xét ∆OAB có OA = OB nên ∆OAB cân tại O, lại có nên ∆OAB là tam giác đều. Suy ra AB = OA = OB = 2 cm và

Tương tự, ta chứng minh được ∆OAF là tam giác đều nên

Khi đó hay

Do đó, vì ABCDEF là lục giác đều nên các góc bằng nhau và bằng 120°.

Vậy độ dài các cạnh của lục giác đều bằng 2 centimét và số đo các góc của lục giác đều bằng 120°.

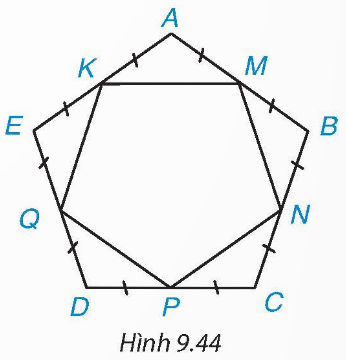
⦁ Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA (1) và

Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA nên     

Từ (1) và (2) suy ra MA = MB = NB = NC = PC = PD = QD = QE = KE = KA.

Xét ∆AKM và ∆BMN có:

AK = BM, AM = BN

Do đó ∆AKM = ∆BMN (c.g.c)

Suy ra KM = MN (hai cạnh tương ứng) và (hai góc tương ứng). (3)

Tương tự, sẽ ta chứng minh được:

∆AKM = ∆BMN = ∆CNP = ∆DPQ = ∆EQK.

Suy ra KM = MN = NP = PQ = QK. (8)

⦁ Xét ∆AKM có AK = AM nên ∆AKM cân tại A, suy ra

Từ (3) và (4) suy ra

Chứng minh tương tự như trên ta có:

Ta có

Suy ra nên

Tương tự, ta chứng minh được:

Từ (5), (6) và (7) suy ra

Từ (8) và (9) suy ra MNPQK có các cạnh bằng nhau và các góc bằng nhau.

Vậy MNPQK là ngũ giác đều.

Cách 1:

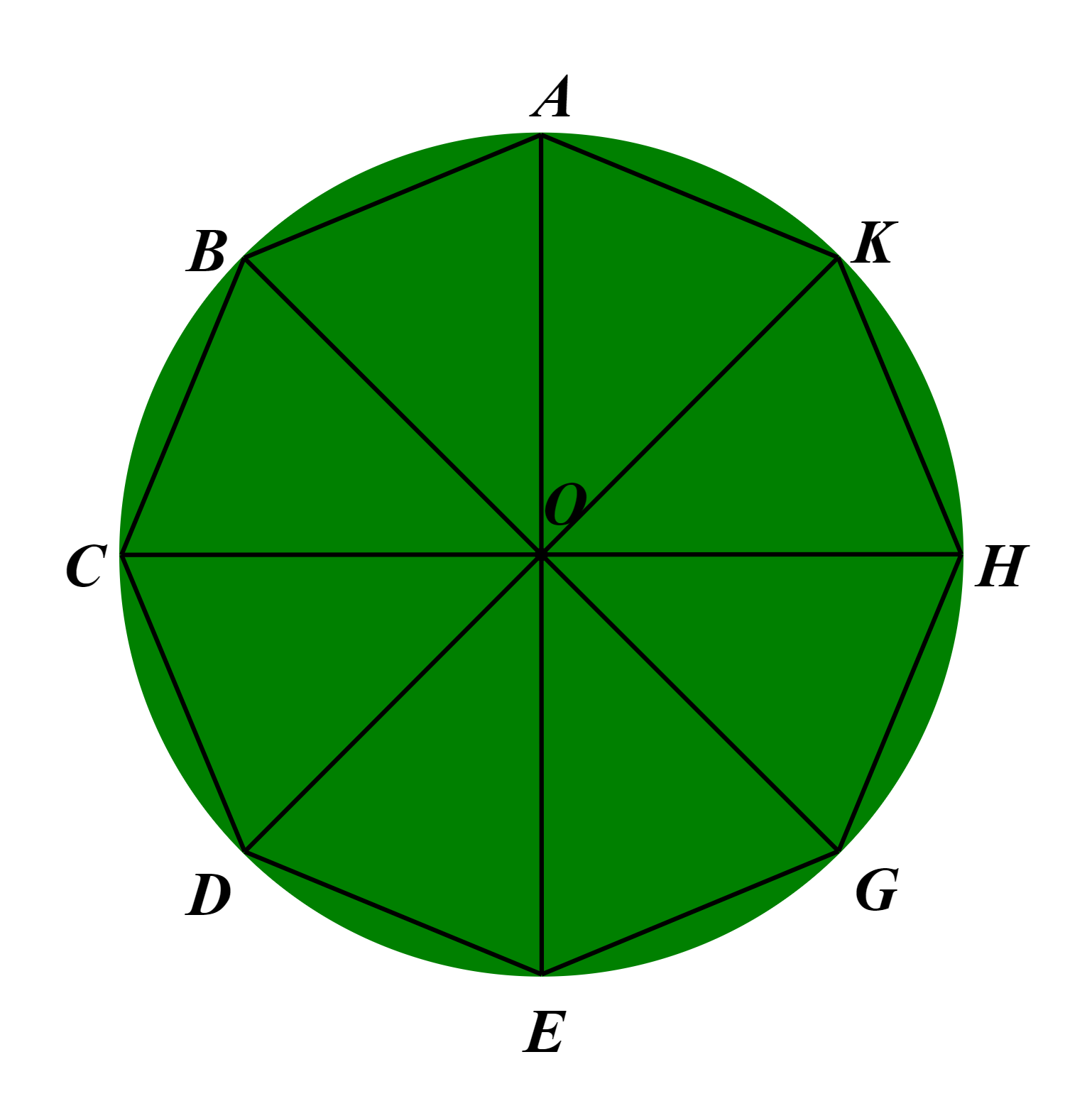
Giả sử ABCDEGHK là bát giác đều nội tiếp đường tròn (O).

Do đó AB = BC = CD = DE = EG = GH = HK và OA = OB = OC = OD = OE = OG = OH = OK.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC

Do đó ∆OAB = ∆OBC (c.c.c).

Tương tự, ta sẽ chứng minh được:

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.

Suy ra các góc tương ứng bằng nhau:

Ta có:

Suy ra nên

Lại có (tổng ba góc của ∆OAB bằng 180°)

Suy ra

Vì ∆AOB = ∆OKA nên (hai góc tương ứng).

Suy ra

Do đó, vì ABCDEGHK là bát giác đều nên các góc bằng nhau và bằng 135°.

Cách 2:

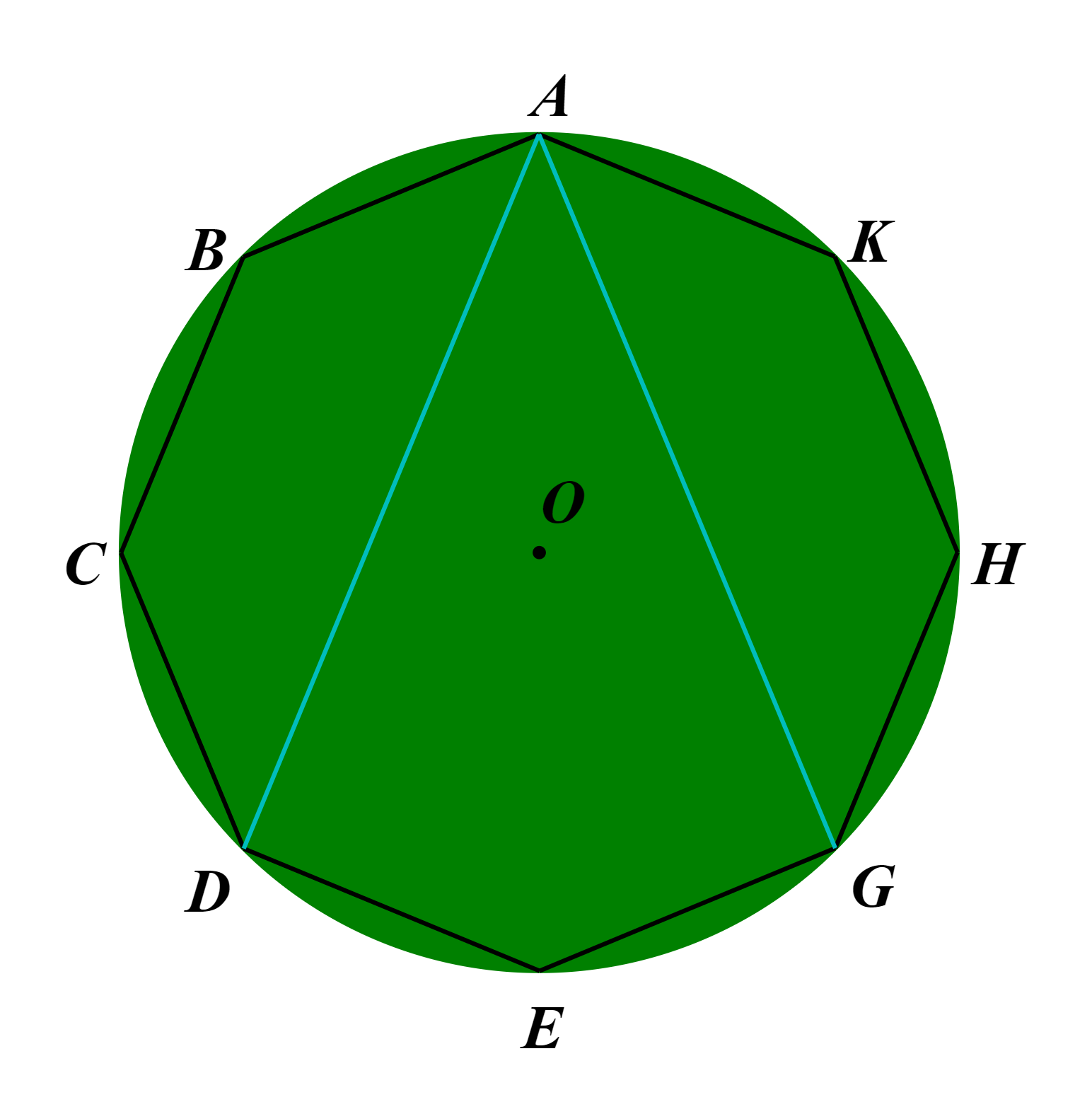
Bát giác đều ABCDEGHK được chia thành ba tứ giác ABCD, ADEG và AGHG.

Ta thấy tổng số đo các góc của bát giác ABCDEGHK bằng tổng số đo các góc của ba tứ giác kể trên.

Mà mỗi tứ giác có tổng số đo các góc bằng 360°, do đó tổng số đo các góc của bát giác đều ABCDEGHK là: 3.360° = 1 080°.

Vì ABCDEGHK là bát giác đều nên 8 góc của bát giác bằng nhau và mỗi góc có số đo bằng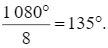

Vậy mỗi góc của bát giác đều có số đo bằng 135°.

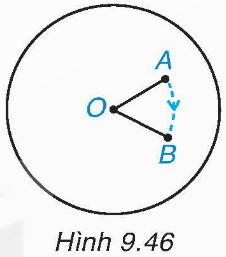
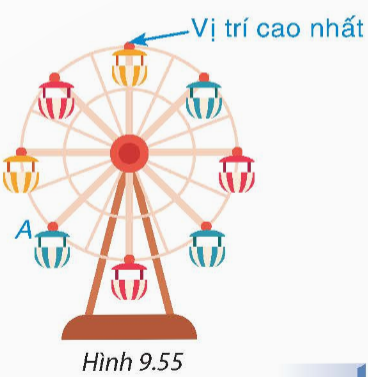
Khi quay bàn xoay thì khoảng cách từ tâm O đến chiếc cốc không thay đổi nên OA = OB. Do đó khoảng cách từ hai điểm A và B đến điểm O bằng nhau.

Vì OA = OB nên hai điểm A, B cùng nằm trên đường tròn tâm O.

Vì tam giác ABC đều nên AB = BC = CA.

Vì tam giác ABC nội tiếp đường tròn (O) nên OA = OB = OC.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC

Do đó ∆OAB = ∆OBC (c.c.c)

Suy ra (hai góc tương ứng).

Vì vậy, nếu quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A di chuyển đến vị trí của điểm B và sẽ di chuyển trên cung tròn AB của đường tròn (O).

Khi đó, tia OB di chuyển trùng với tia OC (ở vị trí ban đầu), tia OC di chuyển trùng với tia OA (ở vị trí ban đầu). Vậy điểm C sẽ di chuyển đến vị trí của điểm A.