khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

22/08/2024 4,631 Lưu

Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là 240 cm.

Gọi x là độ dài cạnh của thiết diện ngang.

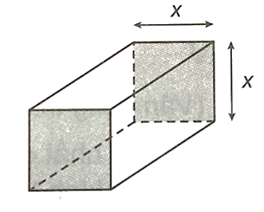
Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là 240 cm. Gọi x là độ dài cạnh của thiết diện ngang. (ảnh 1)

a) Tính thể tích của khối bưu kiện theo x.

b) Kí hiệu V(x) là thể tích của khối bưu kiện. Khảo sát sự biến thiên của hàm số y = V(x).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Chu vi thiết diện ngang là: 4x (cm).

Chiều dài của khối bưu kiện là: 240 – 4x (cm).

Do đó, thể tích của khối bưu kiện là: V(x) = (240 – x)x2 (cm3).

b) Khảo sát sự biến thiên của hàm số y = V(x).

1. Tập xác định là: (0; 60).

2. Sự biến thiên:

Ta có: V'(x) = 480x – 12x2

           V'(x) = 0 ⇔ x = 40 (do x > 0).

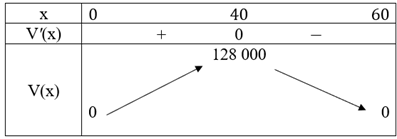
Hàm số đồng biến trên khoảng (0; 40), nghịch biến trên khoảng (40; 60).

Hàm số đạt cực đại tại x = 40 với VCĐ = 128 000 (cm3).

Ta có bảng biến thiên như sau:

Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là 240 cm. Gọi x là độ dài cạnh của thiết diện ngang. (ảnh 2)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x2 + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị sản phẩm là \[f\left( x \right) = \frac{{C(x)}}{x}.\]

a) Khảo sát sự biến thiên của hàm số y = f(x).

b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?

Lời giải

a) Ta có: \[f\left( x \right) = \frac{{C(x)}}{x}\] = 0,2x + 10 + \(\frac{5}{x}\) với x ≥ 1.

                f'(x) = 0,2 – \(\frac{5}{{{x^2}}}\)

                f'(x) = 0 ⇔ 0,2 – \(\frac{5}{{{x^2}}}\) = 0 ⇔ x = 5 (do x ≥ 1).

Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).

Ta có bảng biến thiên như sau:

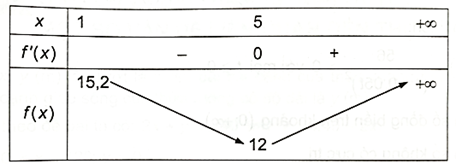
Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x^2 + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị (ảnh 1)

Hàm số đồng biến trên khoảng (5; +∞), nghịch biến trên khoảng (1; 5).

Hàm số đạt cực đại tại x = 5 với fCT = 12.

Câu 2

Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu ó 80 000 con. Sau t năm, số lượng quần thể cá nói trên được xác định bởi

N(t) = \(\frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\) (nghìn con).

a) Khảo sát sự biến thiên của hàm số y = N(t).

b) Số lượng tối đa có thể có của quần thể cá là bao nhiêu?

Lời giải

a) Khảo sát sự biến thiên của hàm số y = N(t).

1. Tập xác định: [0; +∞).

2. Sự biến thiên

Ta có: N(t) = \(\frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\)

           N'(t) = \(\frac{{56}}{{{{\left( {1 + 0,05t} \right)}^2}}} > 0\) với mọi t ≥ 0.

Hàm số đồng biến trên khoảng (0; +∞).

Hàm số không có cực trị.

Giới hạn tại vô cực: \(\mathop {\lim }\limits_{t \to + \infty } N(t)\) = 1200.

Bảng biến thiên:

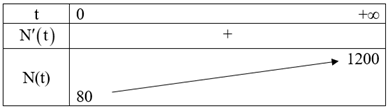
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu ó 80 000 con. Sau t năm, số lượng quần thể cá nói trên được xác định bởi (ảnh 1)

b) Số lượng tối đa có thể có của quần thể cá là 1 200 000 con.

Câu 3

Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 là một hàm liên tục có đồ thị như hình sau:

Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 là một hàm liên tục có đồ thị như hình sau: a) Lập bảng biến thiên của hàm vận tốc y = v(t) của vật, với t ∈ [1; 5]. b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất? (ảnh 1)

a) Lập bảng biến thiên của hàm vận tốc y = v(t) của vật, với t ∈ [1; 5].

b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho điểm A(3;2 ) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC nằm trong góc phần tư thứ nhấ, với O là gốc tọa độ.

Cho điểm A(3;2 ) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC nằm (ảnh 1)

a) Biết hoành độ điểm B là x = t với t > 3. Tính diện tích tam giác OBC theo t. Kí hiệu diện tích này là S(t).

b) Khảo sát sự biến thiên của hàm số S(t).

c) Tìm vị trí điểm B để diện tích tam giác OBC là nhỏ nhất.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích 300 cm2, lề trái và lề phải là 2 cm, lề trên và lề dưới là 3 cm. Gọi x (cm) là chiều rộng của tờ giấy.

a) Tính diện tích của tờ giấy theo x.

b) Kí hiệu diện tích tờ giấy là S(x). Khảo sát sự biến thiên của hàm số y = S(x).

c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y = f(x) có đạo hàm f'(x) xác định trên ℝ và f'(x) có đồ thị như hình vẽ sau:

Cho hàm số y = f(x) có đạo hàm f'(x) xác định trên ℝ và f'(x) có đồ thị như hình vẽ sau: Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số y = f(x). (ảnh 1)

Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số y = f(x).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) \(y = \frac{{{x^2} - 4x + 8}}{{x - 2}};\)

b) \(y = \frac{{2{x^2} + 3x - 5}}{{x + 1}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập