Cho hàm số \(y = \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}}\). Mệnh đề nào sau đây là đúng?
A. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
B. Đồ thị hàm số có hai đường tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.
Cho hàm số \(y = \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}}\). Mệnh đề nào sau đây là đúng?
A. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
B. Đồ thị hàm số có hai đường tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}} = 2\); \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}} = 2\)
Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to 5} y = \mathop {\lim }\limits_{x \to 5} \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{2{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x - 5} \right)}} = \mathop {\lim }\limits_{x \to 5} \frac{{2\left( {x - 1} \right)}}{{x - 5}} = + \infty \);
\(\mathop {\lim }\limits_{x \to 1} y = \mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} - 4x + 2}}{{{x^2} - 6x + 5}} = \mathop {\lim }\limits_{x \to 1} \frac{{2{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x - 5} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{2\left( {x - 1} \right)}}{{x - 5}} = 0\).
Do đó, đường thẳng x = 5 là đường tiệm cận đứng của đồ thị hàm số.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Tập xác định: D = ℝ.
Ta có: y' = 3x2 – 6x2
y' = 0 ⇔ 3x2 – 6x2 = 0 ⇔ x = 0 hoặc x = 2.
Hàm số đồng biến trên khoảng (−∞; 0) và (2; +∞).
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại điểm x = 0 và yCĐ = y(0) = 2.
Hàm số đạt cực tiểu tại điểm x = 2 và yCT = y(2) = −2.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
Ta có bảng biến thiên như sau:
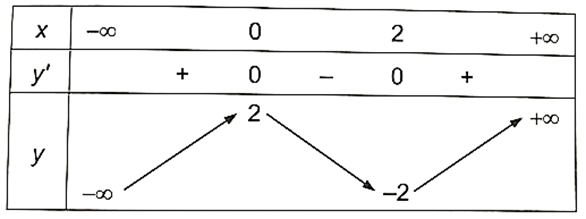
Đồ thị hàm số đi qua các điểm: (3; 2); (2; −2); (−1; −2); (0; 2).
Đồ thị hàm số có tâm đối xứng là điểm (1; 0).
Đồ thị hàm số như sau:
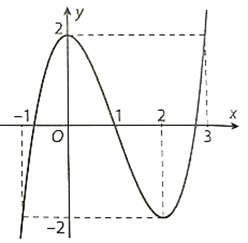
b) Tâm đối xứng của đồ thị hàm số là điểm I(1; 0).
Ta có: y'(1) = −3.
Vậy phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó là:
y = y'(1)(x – 1) + y(1)
= −3(x – 1) + 0
= −3x + 3 (∆).
Ta có: y' = 3x2 – 6x = 3(x2 – 2x + 1) – 3 = 3(x – 1)2 – 3 ≥ −3 với mọi x.
Vậy ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).
c) Ta có: x3 – 3x2 – m = 0 ⇔ x3 – 3x2 + 2 = m + 2.
Vậy phương trình x3 – 3x2 – m = 0 là phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng y = m + 2. Suy ra, phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y = m + 2 cắt đồ thị (C) tại 3 điểm phân biệt, điều này tương đương với −2 < m + 2 < 2 ⇔ −4 < m < 0.Lời giải
a) Ta có:
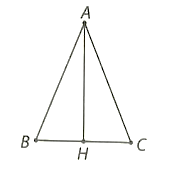
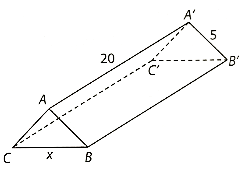
Kẻ AH là chiều cao của tam giác ABC
Lúc này, AH = \(\sqrt {A{C^2} - H{C^2}} \) = \(\sqrt {25 - {{\left( {\frac{x}{2}} \right)}^2}} \) = \(\frac{1}{2}\sqrt {100 - {x^2}} \).
Diện tích tam giác ABC là:
S∆ABC = \(\frac{1}{2}\)BC. AH = \(\frac{1}{2}\)x\(\frac{1}{2}\sqrt {100 - {x^2}} \) = \(\frac{1}{4}x\sqrt {100 - {x^2}} \).
Thể tích khối lăng trụ là:
V = S∆ABC. AA' = 5x\(\sqrt {100 - {x^2}} \) (m3) với 0 < x < 10.
b) Xét hàm số thể tích f(x) = 5x\(\sqrt {100 - {x^2}} \) trên khoảng (0; 10).
Ta có: f'(x) = 5\(\sqrt {100 - {x^2}} \) + 5x.\(\frac{{ - 2x}}{{2\sqrt {100 - {x^2}} }}\) = \(\frac{{500 - 10{x^2}}}{{\sqrt {100 - {x^2}} }}\);
f'(x) = 0 ⇔ x = \(5\sqrt 2 \) (x > 0).
Bảng biến thiên:
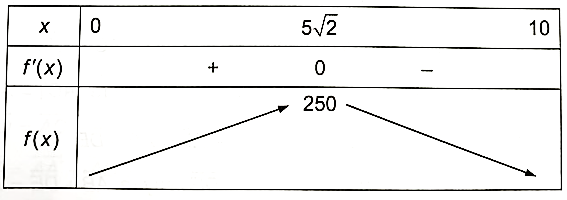
Vậy hình lăng trụ có thể tích lớn nhất khi x = \(5\sqrt 2 \) (m).
Vậy \(\mathop {\max }\limits_{x \in (0;10)} V = V\left( {5\sqrt 2 } \right) = 250\)(m3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.