Giải SBT Toán 12 Tập 1 KNTT Bài tập cuối chương I có đáp án
48 người thi tuần này 4.6 586 lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Cho hàm số y = f(x) có đạo hàm trên (a;b). Xét các mệnh đề sau:
(I) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên
(a; b) thì hàm số đồng biến trên (a; b).
(II) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên (a; b) thì hàm số nghịch biến trên (a; b).
(III) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) thì hàm số nghịch biến trên khoảng (a; b).
(IV) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) thì hàm số đồng biến trên khoảng (a; b).
Trong các mệnh để trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I, II, III và IV đúng.
B. I, II và III đúng, còn IV sai.
C. I, II và IV đúng, còn III sai.
D. I và II đúng, còn III và IV sai.
Cho hàm số y = f(x) có đạo hàm trên (a;b). Xét các mệnh đề sau:
(I) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên
(a; b) thì hàm số đồng biến trên (a; b).
(II) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên (a; b) thì hàm số nghịch biến trên (a; b).
(III) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) thì hàm số nghịch biến trên khoảng (a; b).
(IV) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) thì hàm số đồng biến trên khoảng (a; b).
Trong các mệnh để trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I, II, III và IV đúng.
B. I, II và III đúng, còn IV sai.
C. I, II và IV đúng, còn III sai.
D. I và II đúng, còn III và IV sai.
Lời giải
Đáp án đúng là: D
Mệnh đề đúng là:
(I) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên
(a; b) thì hàm số đồng biến trên (a; b).
(II) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên (a; b) thì hàm số nghịch biến trên (a; b).
Lời giải
Đáp án đúng là: C
Xét đáp án C, ta có: y = \(\frac{{2024}}{{{e^x}}}\) = 2024.e−x
y' = −2024.e−x < 0 với mọi x.
Vậy hàm số y = \(\frac{{2024}}{{{e^x}}}\) nghịch biến trên tập xác định của nó.
Lời giải
Đáp án đúng là: D
Tập xác định: D = ℝ\{−2023}.
Ta có: y' = \(\frac{{2023 - m}}{{{{\left( {x + 2023} \right)}^2}}}\)
Để hàm số đồng biến trên từng khoảng xác định của nó thì \(\frac{{2023 - m}}{{{{\left( {x + 2023} \right)}^2}}}\) > 0,với mọi x ∈ D.
Suy ra 2023 – m > 0 hay m < 2023.
Theo đề bài m là giá trị nguyên dương và m < 2023.
Vậy có 2022 giá trị m thỏa mãn.
Lời giải
Đáp án đúng là: B
Ta có: f'(x) = x(x – 1)2(x + 2)4 = 0
Suy ra x = 0 hoặc x = 1 hoặc x = −2.
Ta có bảng xét dấu như sau:

Vậy hàm số có 1 điểm cực trị.
Lời giải
Đáp án đúng là: A
Tập xác định: D = ℝ\{−m}.
Ta có: y' = \(\frac{{\left( {x + m + 1} \right)\left( {x + m - 1} \right)}}{{{{\left( {x + m} \right)}^2}}}\)
y' = 0 ⇔ \(\frac{{\left( {x + m + 1} \right)\left( {x + m - 1} \right)}}{{{{\left( {x + m} \right)}^2}}}\) = 0 ⇔ x = −m – 1 hoặc x = 1 – m.
Nhận thấy, với mọi m luôn có −m – 1 < 1 – m.
Ta có bảng biến thiên như sau:
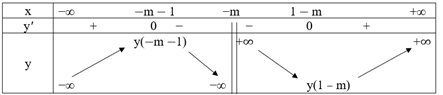
Để hàm số đạt cực đại tại x = 2 thì −m – 1 = 2 hay m = −1.
Vậy m = −1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.