Chọn phương án đúng.
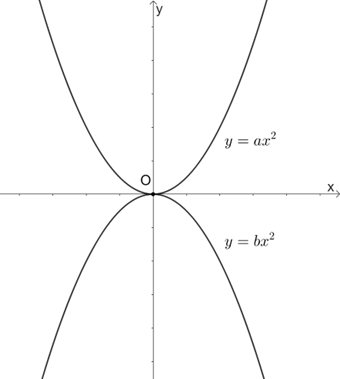
Hình bên là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?
A. a < 0 < b.
B. a < b < 0.
C. a > b > 0.
D. a > 0 > b.
Chọn phương án đúng.
Hình bên là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?

A. a < 0 < b.
B. a < b < 0.
C. a > b > 0.
D. a > 0 > b.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài tập cuối chương 6 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Đồ thị hàm số y = ax2 là hình parabol hướng lên trên và nằm trên trục Ox nên có hệ số a > 0.
Đồ thị hàm số y = bx2 là hình parabol hướng xuống và nằm dưới trục Ox nên có hệ số b < 0.
Vậy a > 0 > b.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (%) là lãi suất năm của hình thức gửi tiết kiệm này. Điều kiện: x > 0.
Sau một năm, số tiền cả vốn lẫn lãi của bác Hương là:
\(100 + 100.\frac{x}{{100}} = 100 + x\) (triệu đồng).
Tổng số tiền bác Hương gửi ở năm thứ hai là: 100 + x + 50 = 150 + x (triệu đồng).
Sau hai năm, số tiền cả vốn lẫn lãi bác Hương nhận được là:
\(150 + x + \left( {150 + x} \right).\frac{x}{{100}}\) (triệu đồng).
Do sau hai năm, bác Hương nhận được số tiền cả vốn lẫn lãi là 176 triệu đồng nên ta có phương trình:
\(150 + x + \left( {150 + x} \right).\frac{x}{{100}} = 176,\) hay \(\frac{{{x^2}}}{{100}} + \frac{5}{2}x - 26 = 0.\)
Giải phương trình này ta được: x = 10 (thỏa mãn điều kiện) hoặc x = −260 (loại).
Vậy lãi suất năm của hình thức gửi tiết kiệm này là 10%.
Lời giải
Đáp án đúng là: D
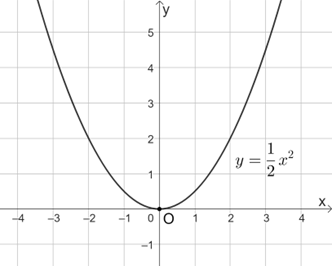
Ta có:
• \(\frac{1}{2}{.1^2} = \frac{1}{2} \ne 2\) nên điểm (1; 2) không thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}.\)
• \(\frac{1}{2}{.2^2} = 2 \ne 1\) nên điểm (2; 1) không thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}.\)
• \(\frac{1}{2}.{\left( { - 2} \right)^2} = 2 \ne 1\) nên điểm (−2; 1) không thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}.\)
• \(\frac{1}{2}.{\left( { - 1} \right)^2} = \frac{1}{2}\) nên điểm \(\left( { - 1;\frac{1}{2}} \right)\) thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}.\)
Vậy điểm thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) là \(\left( { - 1;\frac{1}{2}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.