Chọn phương án đúng.
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6 cm. Khẳng định nào sau đây là đúng về vị trí tương đối của a và đường tròn (O; 9 cm)?
A. Đường thẳng a cắt đường tròn (O) tại hai điểm.
B. Đường thẳng a tiếp xúc với đường tròn (O).
C. Đường thẳng a và đường tròn (O) không có điểm chung.
D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.
Chọn phương án đúng.
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6 cm. Khẳng định nào sau đây là đúng về vị trí tương đối của a và đường tròn (O; 9 cm)?
A. Đường thẳng a cắt đường tròn (O) tại hai điểm.
B. Đường thẳng a tiếp xúc với đường tròn (O).
C. Đường thẳng a và đường tròn (O) không có điểm chung.
D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
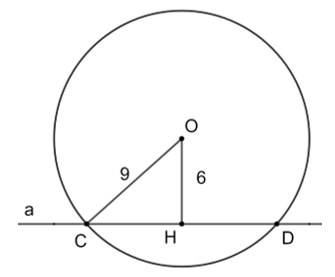
Gọi H là chân đường cao từ O đến đường thẳng a. Do đó, OH = 6 cm.
Vì đường tròn (O) có bán kính R = 9 cm và OH < R nên đường thẳng a cắt đường tròn (O) tại hai điểm.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(H.5.32)
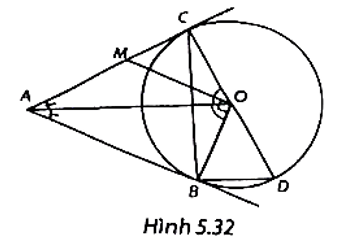
a) Xét hai tiếp tuyến AB, AC của (O) cắt nhau tại A, ta có: AB = AC suy ra A thuộc đường trung trực của đoạn thẳng BC.
Mặt khác, OB = OC (cùng bằng bán kính).
Do đó O thuộc đường trung trực của đoạn thẳng BC.
Vậy AO là đường trung trực của BC.
b) Xét tam giác CBD có BO là đường trung tuyến, \(BO = \frac{1}{2}CD.\)
Suy ra ∆CBD là tam giác vuông, hay BC ⊥ BD.
Mặt khác, AO ⊥ BC (do AO là đường trung trực của BC).
Từ đó suy ra BD // AO.
c) Theo giả thiết, ta có OM ⊥ OB, suy ra \(\widehat {MOA} + \widehat {AOB} = 90^\circ .\) (1)
Ta có \(\widehat {MAO} = \widehat {BAO}\) (do A là giao điểm của hai tiếp tuyến của (O)).
Vì AB là tiếp tuyến của (O) nên OB ⊥ AB. Do đó \[\widehat {BAO} + \widehat {AOB} = 90^\circ .\] (2)
Từ (1) và (2) suy ra \[\widehat {MOA} = \widehat {MAO},\] do đó ∆AMO là tam giác cân.
Suy ra MO = MA (điều phải chứng minh).
Lời giải
(H.5.31)
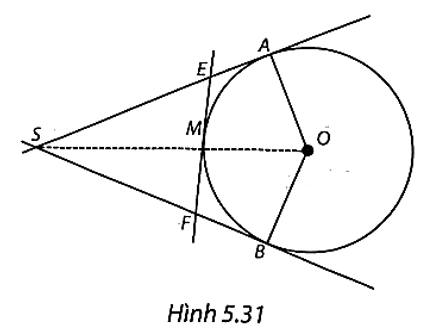
a) Xét hai tiếp tuyến của (O) cắt nhau tại E ta có EA = EM. Tương tự, có FB = FM.
Chu vi của tam giác SEF là
\({P_{SEF}} = SE + EF + SF = SE + \left( {EM + MF} \right) + SF\)
\( = SE + EA + FB + SF = \left( {SE + EA} \right) + \left( {FB + SF} \right)\)
= SA + SB (điều phải chứng minh).
b) Giả sử M trùng với giao điểm của SO và (O).
Xét hai tiếp tuyến SA, SB của (O) cắt nhau tại S, ta có: SA = SB và SO là tia phân giác của \(\widehat {ASB}.\)
Tam giác SAB cân tại S (do SA = SB) có SO là đường phân giác nên đồng thời đường trung trực, tức là đoạn thẳng EF là tiếp tuyến của (O) tại M nên OM ⊥ EF, do đó SO ⊥ EF.
Từ đó suy ra AB // EF (cùng vuông góc với SO).
Tam giác SAB có AB // EF nên \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) mà SA = SB, do đó SE = SF (điều phải chứng minh).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo