Để chở hết 60 tấn hàng, một đội xe dự định sử dụng một số xe cùng loại. Trước khi khởi hành, có 2 xe được điều động đi làm việc khác, vì vậy mỗi xe còn lại phải chở nhiều hơn dự định 1 tấn hàng. Hỏi lúc đầu đội dự định dùng bao nhiêu xe?
Quảng cáo
Trả lời:
Số hàng mỗi xe dự định chở là: \(\frac{{60}}{x}\) (tấn).
Số xe thực tế đội dùng là \[x--2\](xe).
Số hàng thực tế mỗi xe chở là: \(\frac{{60}}{{x - 2}}\) (tấn).
Vì mỗi xe phải chở nhiều hơn 1 tấn hàng so với dự định nên ta có phương trình:
\(\frac{{60}}{{x - 2}} - \frac{{60}}{x} = 1\)
\( \Rightarrow 60x - 60\left( {x - 2} \right) = x\left( {x - 2} \right)\)
\( \Leftrightarrow 60x - 60x + 120 = {x^2} - 2x\)
\( \Leftrightarrow {x^2} - 2x - 120 = 0\)
Giải phương trình được \({x_1} = \) 12 (thỏa mãn đk) \({x_2} = - 10\) (Không thỏa mãn đk)
Kết luận số xe dự định dùng là 12 xe.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
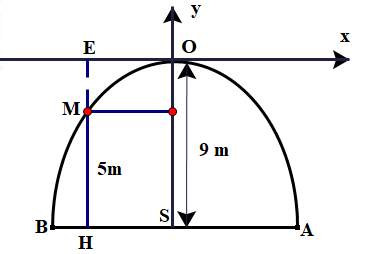
\({\rm{B}}( - 3; - 9) \in (P):y = a{x^2} \Rightarrow - 9 = a \cdot {( - 3)^2} \Rightarrow a = - 1\)
\((P):y = - {x^2}\)
Khi banh đạt độ cao 5 m thì \({\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 9 - 5 = 4\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_M}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = - \sqrt 4 = - 2\)
Vậy sau 1 giây kể từ khi bóng được đá lên thì đạt độ cao 5 m.
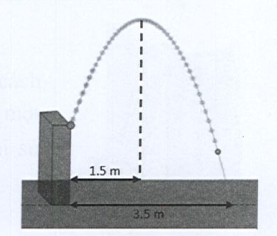
Lời giải
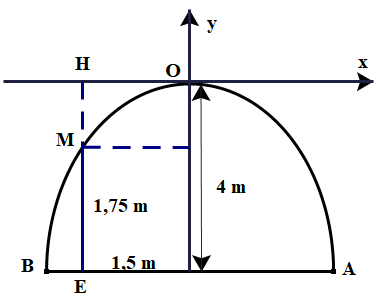
\({\rm{MH}} = {\rm{HE}} - {\rm{ME}} = 4 - 1,75 = 2,25\)
\( \Rightarrow {\rm{M}}( - 1,5; - 2,25) \in (P):y = a{x^2}\)\( \Rightarrow - 2,25 = a \cdot {( - 1,5)^2} \Rightarrow a = \frac{{ - 2,25}}{{{{( - 1,5)}^2}}} = - 1\)\((P):y = - {x^2}\)
\( \Rightarrow {\rm{A}}\left( {{x_A}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = \sqrt 4 = 2\;{\rm{m}}\)
\({\rm{EA}} = {\rm{ES}} + {\rm{SA}} = 2 + 1,5 = 3,5\)
Vậy nước rơi xuống đất cách chân tháp một khoảng là \(3,5\;{\rm{m}}\).
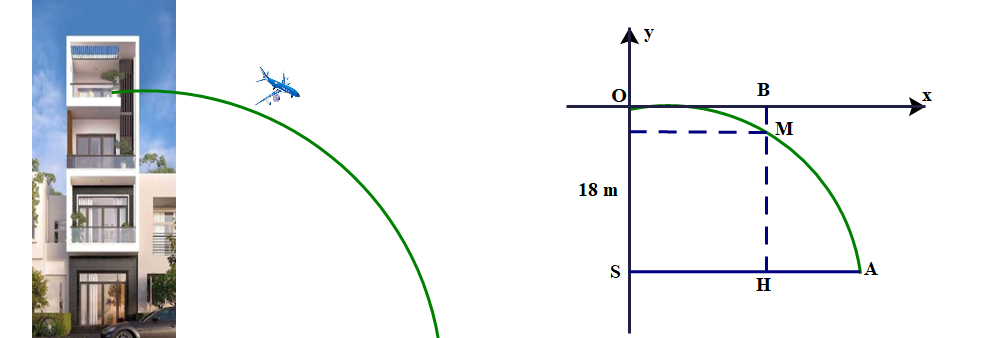
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
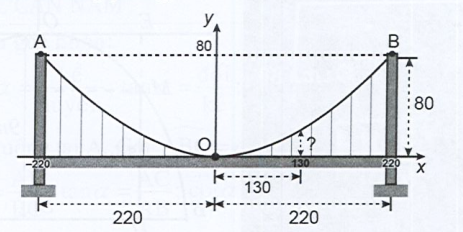
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.