Để chở hết 120 tấn khoai lang ủng hộ bà con nông dân huyện Bình Sơn, tỉnh Quảng Ngãi vượt qua khó khăn do ảnh hưởng của đại dịch viêm đường hô hấp cấp nCovid – 19, một đội xe dự định dùng một số xe cùng loại. Lúc sắp khởi hành đội được bổ sung thêm 5 xe cùng loại, vì vậy so với dự định mỗi xe phải chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe?
Quảng cáo
Trả lời:
Số tấn khoai lang mỗi xe dự định phải chở là \(\frac{{120}}{x}\) (tấn)
Số xe lúc sau của đội là \(x + 5\) (xe)
Số tấn khoai lang mỗi xe thực tế phải chở là \(\frac{{120}}{{x + 5}}\) (tấn)
Vì so với dự định thực tế mỗi xe phải chở ít hơn 2 tấn nên ta có phương trình
\(\frac{{120}}{x} - \frac{{120}}{{x + 5}} = 2\)
\( \Leftrightarrow {x^2} + 5x - 300 = 0\).
Giải phương trình \({x^2} + 5x - 300 = 0\)
\(\Delta = 25 + 4.300\)\( = 1225\)
Vì \(\Delta > 0\)nên phương trình có hai nghiệm phân biệt
\({x_1} = \frac{{ - 5 + \sqrt {1225} }}{2} = 15\); \({x_2} = \frac{{ - 5 - \sqrt {1225} }}{2} = - 20\)
Đối chiếu với điều kiện của ẩn và kết luận số xe lúc đầu của đội là \(15\) xe.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
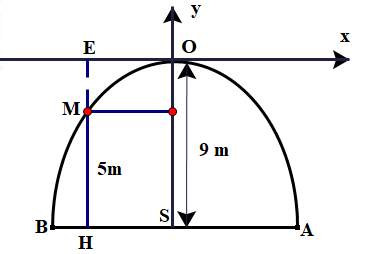
\({\rm{B}}( - 3; - 9) \in (P):y = a{x^2} \Rightarrow - 9 = a \cdot {( - 3)^2} \Rightarrow a = - 1\)
\((P):y = - {x^2}\)
Khi banh đạt độ cao 5 m thì \({\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 9 - 5 = 4\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_M}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = - \sqrt 4 = - 2\)
Vậy sau 1 giây kể từ khi bóng được đá lên thì đạt độ cao 5 m.
Lời giải
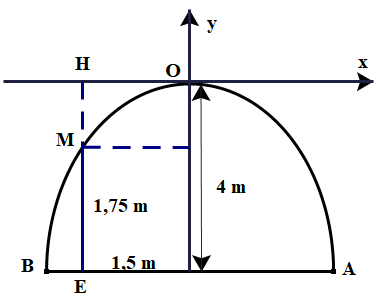
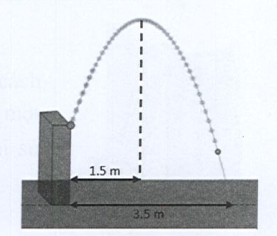
\({\rm{MH}} = {\rm{HE}} - {\rm{ME}} = 4 - 1,75 = 2,25\)
\( \Rightarrow {\rm{M}}( - 1,5; - 2,25) \in (P):y = a{x^2}\)\( \Rightarrow - 2,25 = a \cdot {( - 1,5)^2} \Rightarrow a = \frac{{ - 2,25}}{{{{( - 1,5)}^2}}} = - 1\)\((P):y = - {x^2}\)
\( \Rightarrow {\rm{A}}\left( {{x_A}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = \sqrt 4 = 2\;{\rm{m}}\)
\({\rm{EA}} = {\rm{ES}} + {\rm{SA}} = 2 + 1,5 = 3,5\)
Vậy nước rơi xuống đất cách chân tháp một khoảng là \(3,5\;{\rm{m}}\).
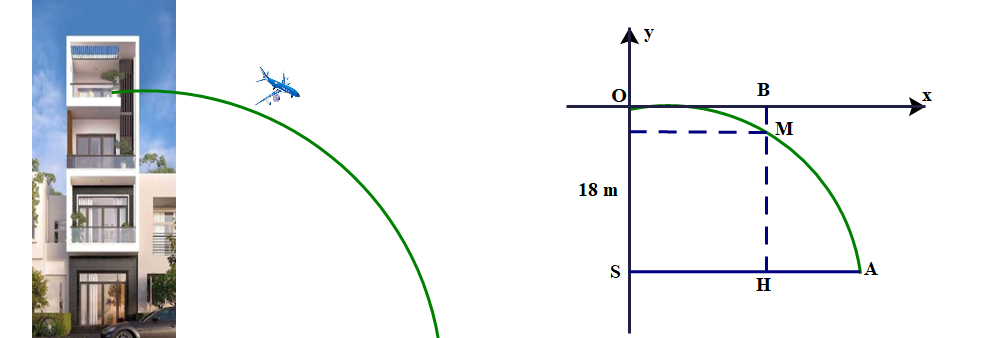
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
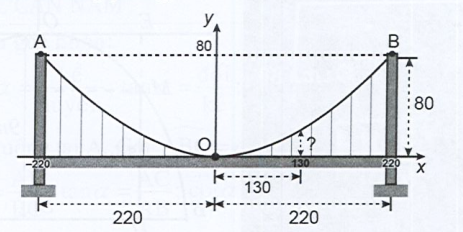
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.