Một đoàn xe vận tải dự định điều một số xe cùng loại để vận chuyển 40 tấn hàng. Lúc sắp khởi hành đoàn xe được giao thêm 14 tấn nữa. Do đó phải điều thêm 2 xe cùng loại trên và mỗi xe phải chở thêm 0,5 tấn. Tìm số lượng xe phải điều theo dự định, biết mỗi xe đều chở số lượng hàng như nhau và mỗi xe chở không quá 3 tấn hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong thực tế, mỗi xe phải chở số tấn hàng là: \(x + 0,5\) (tấn).
Số xe phải điều theo dự định là: \(\frac{{40}}{x}\) (xe).
Số xe được sử dụng theo thực tế là: \(\frac{{54}}{{x + 0,5}}\) (xe).
Vì thực tế phải điều thêm 2 xe so với dự định nên ta có phương trình:
\(\frac{{54}}{{x + 0,5}} - \frac{{40}}{x} = 2\)
\( \Leftrightarrow \frac{{54x}}{{x\left( {x + 0,5} \right)}} - \frac{{40\left( {x + 0,5} \right)}}{{x\left( {x + 0,5} \right)}} = \frac{{2x\left( {x + 0,5} \right)}}{{x\left( {x + 0,5} \right)}}\)
\( \Rightarrow 54x - 40\left( {x + 0,5} \right) = 2x\left( {x + 0,5} \right)\)
\( \Leftrightarrow 14x - 20 = 2{x^2} + x\)
\( \Leftrightarrow 2{x^2} - 13x + 20 = 0\)
\( \Leftrightarrow \left( {2x - 5} \right)\left( {x - 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{5}{2}\left( {tm} \right)\\x = 4\left( {ktm} \right)\end{array} \right.\)
Vậy số xe phải điều theo dự định là: \(\frac{{40}}{{2,5}} = 16\) (xe).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
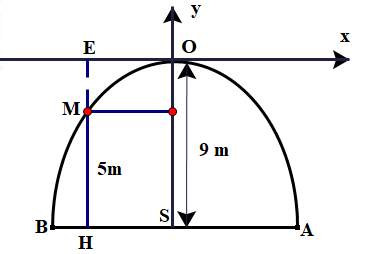
\({\rm{B}}( - 3; - 9) \in (P):y = a{x^2} \Rightarrow - 9 = a \cdot {( - 3)^2} \Rightarrow a = - 1\)
\((P):y = - {x^2}\)
Khi banh đạt độ cao 5 m thì \({\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 9 - 5 = 4\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_M}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = - \sqrt 4 = - 2\)
Vậy sau 1 giây kể từ khi bóng được đá lên thì đạt độ cao 5 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
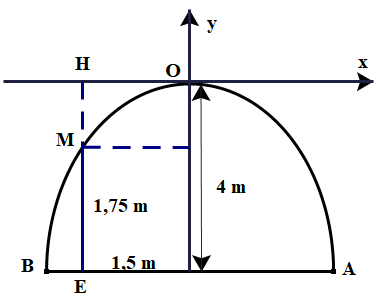
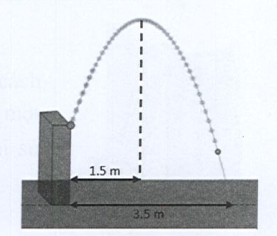
\({\rm{MH}} = {\rm{HE}} - {\rm{ME}} = 4 - 1,75 = 2,25\)
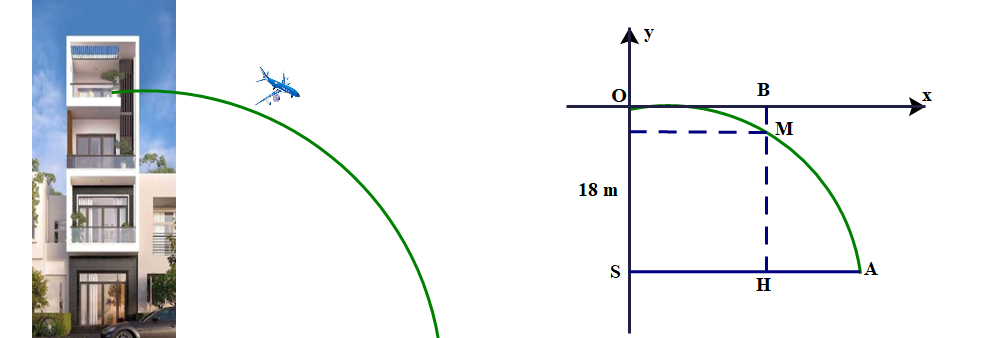
\( \Rightarrow {\rm{M}}( - 1,5; - 2,25) \in (P):y = a{x^2}\)\( \Rightarrow - 2,25 = a \cdot {( - 1,5)^2} \Rightarrow a = \frac{{ - 2,25}}{{{{( - 1,5)}^2}}} = - 1\)\((P):y = - {x^2}\)
\( \Rightarrow {\rm{A}}\left( {{x_A}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = \sqrt 4 = 2\;{\rm{m}}\)
\({\rm{EA}} = {\rm{ES}} + {\rm{SA}} = 2 + 1,5 = 3,5\)
Vậy nước rơi xuống đất cách chân tháp một khoảng là \(3,5\;{\rm{m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập