Câu hỏi:
05/06/2025 21
Hai điểm sáng M và N cùng dao động điều hòa trên trục Ox với phương trình lần lượt là
\({x_M} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{{2\pi }}{3}} \right)\,\,{\rm{cm}}\) và \({x_N} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{3}} \right)\,\,{\rm{cm}}\).
a) Biên độ dao động tổng hợp của hai điểm sáng M và N là \(4\sqrt 2 .\)
b) Khoảng cách của M và N dao động với phương trình là \(4\sqrt 3 \cos \left( {\frac{{5\pi }}{3}t + \pi } \right)\).
c) Khoảng cách lớn nhất của M và N trong quá trình chúng dao động là \(4.\)
d) Kể từ \(t = 0\), thời điểm M và N gặp nhau lần thứ 2025 là \(1211,8\)s.
Hai điểm sáng M và N cùng dao động điều hòa trên trục Ox với phương trình lần lượt là
\({x_M} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{{2\pi }}{3}} \right)\,\,{\rm{cm}}\) và \({x_N} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{3}} \right)\,\,{\rm{cm}}\).
a) Biên độ dao động tổng hợp của hai điểm sáng M và N là \(4\sqrt 2 .\)
b) Khoảng cách của M và N dao động với phương trình là \(4\sqrt 3 \cos \left( {\frac{{5\pi }}{3}t + \pi } \right)\).
c) Khoảng cách lớn nhất của M và N trong quá trình chúng dao động là \(4.\)
d) Kể từ \(t = 0\), thời điểm M và N gặp nhau lần thứ 2025 là \(1211,8\)s.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dao động tổng hợp là \(x = {x_M} + {x_N} = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{{2\pi }}{3}} \right) + 4\cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{3}} \right) = 4\sqrt 3 \cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{2}} \right)\)
Biên độ dao động tổng hợp của hai điểm sáng M và N là \(4\sqrt 3 .\)
Khoảng cách của M và N trong quá trình chúng dao động là
\(d = 4\cos \left( {\frac{{5\pi }}{3}t + \frac{{2\pi }}{3}} \right) - 4\cos \left( {\frac{{5\pi }}{3}t + \frac{\pi }{3}} \right) = - 4\sin \left( {\frac{{5\pi }}{3}t + \frac{\pi }{2}} \right) = 4\cos \left( {\frac{{5\pi }}{3}t + \pi } \right)\)
Khoảng cách lớn nhất của M và N trong quá trình chúng dao động là \(4.\)
Để M, N gặp nhau khi \(d = 0\).
Trong 1 chu kì, M và N gặp nhau 2 lần.
Trong 2012 chu kì đầu, 2 vật gặp nhau 2024 lần
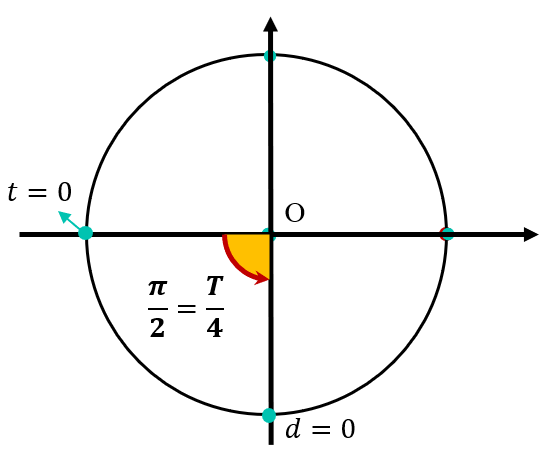
Thời gian lần cuối hai vật gặp nhau là \(\frac{T}{4}\). Vì ta có hình bên:
Vậy sau \(2012T + \frac{T}{4} = 2012,25.\frac{6}{5} = 1214,7\) (s)
Đáp án: a) Sai, b) Sai, c) Đúng, d) Sai.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi \(t = 5\), ta có: \(h\left( 5 \right) = 75\sin \left( {\frac{{\pi \cdot 5}}{8}} \right) \approx 69,3\,\,{\rm{(cm)}}\).
Khi \(t = 20\), ta có: \(h\left( {20} \right) = 75\sin \left( {\frac{{\pi \cdot 20}}{8}} \right) = 75\,\,{\rm{(cm)}}\).
Ta có \(\sin \left( {\frac{{\pi t}}{8}} \right) \le 1 \Rightarrow 75\sin \left( {\frac{{\pi t}}{8}} \right) \le 75\) hay \(h\left( t \right) \le 75\).
Giá trị lớn nhất của \(h\left( t \right)\) là 75, khi đó \(\sin \left( {\frac{{\pi t}}{8}} \right) = 1 \Rightarrow \frac{{\pi t}}{8} = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) \( \Rightarrow t = 4 + 16k\left( {k \in \mathbb{Z}} \right)\).
Vì \(t \in \left[ {0\,;30} \right] \Rightarrow t \in \left\{ {4\,;20} \right\}\) (ứng với \(k\) bằng 0 và 1).
Vậy tại các thời điểm 4 giây hoặc 20 giây (trong 30 giây đầu tiên) thì cơn sóng đạt chiều cao cực đại (là \(75\;\,{\rm{cm}}\)).
Đáp án: a) Đúng, b) Đúng, c) Sai, d) Sai.
Lời giải
Ta có \(f\left( {\frac{\pi }{8}} \right) = \tan \frac{\pi }{4} - 1 = 0\).
Điều kiện xác định: \(2x \ne \frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z} \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2},\,k \in \mathbb{Z}\).
Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}|k \in \mathbb{Z}} \right\}\) và tập giá trị của hàm số là \[\mathbb{R}.\]
Ta có \(f\left( { - x} \right) = \tan \left( { - 2x} \right) - 1 = - \tan 2x - 1\) nên hàm số \(f\left( x \right)\) không chẵn không lẻ.
Ta có \(f\left( {x + \pi } \right) = \tan \left( {2x + \pi } \right) - 1 = \tan 2x - 1 = f\left( x \right)\).
Vậy hàm số \(f\left( x \right)\) là hàm tuần hoàn với chu kì \(\pi \).
Đáp án: a) Đúng, b) Sai, c) Sai, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận